Page 84 - Concise Encyclopedia of Robotics

Derivative
which it rests, and the time of day or night, do not matter; the rendition
is based entirely on the range as a function of the direction in three-
dimensional space.
See also COMPUTER MAP and RANGE SENSING AND PLOTTING.
DERIVATIVE
The term derivative refers to the rate of change of a mathematical function.
For example, speed or velocity is the derivative of displacement, and
acceleration is the derivative of velocity.
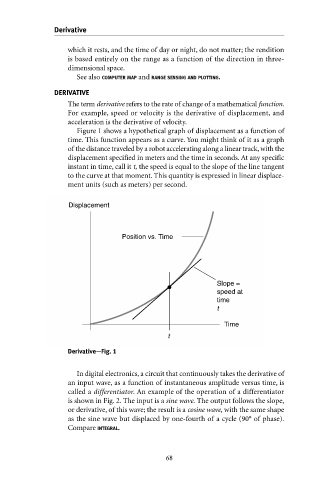
Figure 1 shows a hypothetical graph of displacement as a function of
time. This function appears as a curve. You might think of it as a graph
of the distance traveled by a robot accelerating along a linear track,with the
displacement specified in meters and the time in seconds. At any specific
instant in time, call it t, the speed is equal to the slope of the line tangent
to the curve at that moment. This quantity is expressed in linear displace-
ment units (such as meters) per second.
Displacement
Position vs. Time

Slope =
speed at
time
t
Time
t
Derivative—Fig. 1

In digital electronics, a circuit that continuously takes the derivative of
an input wave, as a function of instantaneous amplitude versus time, is
called a differentiator. An example of the operation of a differentiator
is shown in Fig. 2. The input is a sine wave. The output follows the slope,
or derivative, of this wave; the result is a cosine wave, with the same shape
as the sine wave but displaced by one-fourth of a cycle (90° of phase).
Compare INTEGRAL.

