Page 377 - Control Theory in Biomedical Engineering

Tunable stiffness using negative Poisson's ratio 343

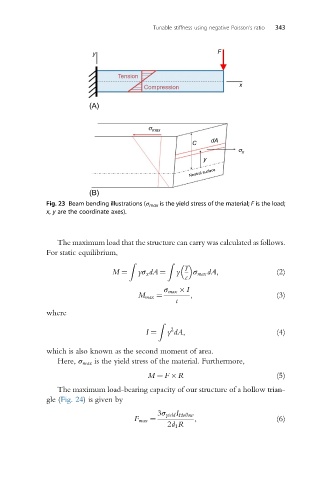
y F

Tension
x
Compression
(A)

s max

C dA
s x
y
Neutral surface

(B)
Fig. 23 Beam bending illustrations (σ max is the yield stress of the material; F is the load;
x, y are the coordinate axes).

The maximum load that the structure can carry was calculated as follows.
For static equilibrium,
Z Z
y

M ¼ yσ x dA ¼ y σ max dA, (2)
c
σ max I
M max ¼ , (3)
c
where

Z
2
I ¼ y dA, (4)
which is also known as the second moment of area.
Here, σ max is the yield stress of the material. Furthermore,

M ¼ F R (5)
The maximum load-bearing capacity of our structure of a hollow trian-
gle (Fig. 24) is given by

3σ yield I Hollow
F max ¼ , (6)
2d 1 R