Page 324 - Decision Making Applications in Modern Power Systems

Decision-making-based optimal generation-side Chapter | 11 285

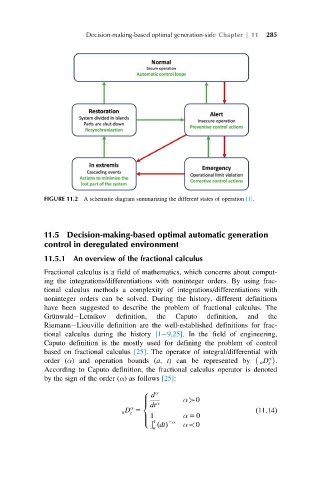
FIGURE 11.2 A schematic diagram summarizing the different states of operation [1].

11.5 Decision-making-based optimal automatic generation
control in deregulated environment
11.5.1 An overview of the fractional calculus

Fractional calculus is a field of mathematics, which concerns about comput-
ing the integrations/differentiations with noninteger orders. By using frac-
tional calculus methods a complexity of integrations/differentiations with
noninteger orders can be solved. During the history, different definitions
have been suggested to describe the problem of fractional calculus. The
Gru ¨nwald Letnikov definition, the Caputo definition, and the
Riemann Liouville definition are the well-established definitions for frac-
tional calculus during the history [1 9,25]. In the field of engineering,
Caputo definition is the mostly used for defining the problem of control
based on fractional calculus [25]. The operator of integral/differential with
α
order (α) and operation bounds (a, t) can be represented by a D .
t
According to Caputo definition, the fractional calculus operator is denoted
by the sign of the order (α) as follows [25]:
d
8 α
> αg0
> dt α
<
α
a D 5 ð11:14Þ
t
> 1 α 5 0
>
Ð t
dt
: 2α
ðÞ α!0
a