Page 145 - Distillation theory

P1: JPJ/FFX P2: FCH/FFX QC: FCH/FFX T1: FCH
0521820928c05 CB644-Petlyuk-v1 June 11, 2004 20:15

5.2 Calculation of Distillation at Minimum Reflux for Ideal Mixtures 119

R
lim
24

20

3
R
lim
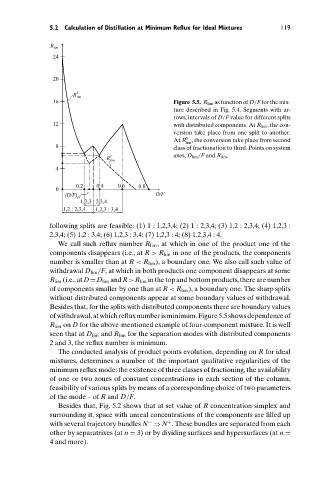
16 Figure 5.5. R lim as function of D/F for the mix-
ture described in Fig. 5.4. Segments with ar-
rows, intervals of D/F value for different splits
12 with distributed components. At R lim , the con-
version take place from one split to another.
3
At R , the conversion take place from second
lim
8 class of fractionation to third. Points on system
2 axes, D lim /F and R lim .
R lim
4

0.2 0.4 0.6 0.8
0
(D/F) D/F
pr
1,2,3 : 2,3,4
1,2 : 2,3,4 1,2,3 : 3,4
following splits are feasible: (1) 1 : 1,2,3,4; (2) 1 : 2,3,4; (3) 1,2 : 2,3,4; (4) 1,2,3 :
2,3,4; (5) 1,2 : 3,4; (6) 1,2,3 : 3,4; (7) 1,2,3 : 4; (8) 1,2,3,4 : 4.
We call such reflux number R lim , at which in one of the product one of the
components disappears (i.e., at R > R lim in one of the products, the components
number is smaller than at R < R lim ), a boundary one. We also call such value of
withdrawal D lim /F, at which in both products one component disappears at some
R lim (i.e.,atD=D lim andR>R lim inthetopandbottomproducts,therearenumber
of components smaller by one than at R < R lim ), a boundary one. The sharp splits
without distributed components appear at some boundary values of withdrawal.
Besides that, for the splits with distributed components there are boundary values
ofwithdrawal,atwhichrefluxnumberisminimum.Figure5.5showsdependenceof
R lim on D for the above-mentioned example of four-component mixture. It is well
seen that at D lim and R lim for the separation modes with distributed components
2 and 3, the reflux number is minimum.
The conducted analysis of product points evolution, depending on R for ideal
mixtures, determines a number of the important qualitative regularities of the
minimum reflux mode: the existence of three classes of fractioning, the availability
of one or two zones of constant concentrations in each section of the column,
feasibility of various splits by means of a corresponding choice of two parameters
of the mode – of R and D/F.
Besides that, Fig. 5.2 shows that at set value of R concentration simplex and
surrounding it, space with unreal concentrations of the components are filled up
with several trajectory bundles N ⇒ N . These bundles are separated from each
+
−
other by separatrixes (at n = 3) or by dividing surfaces and hypersurfaces (at n =
4 and more).