Page 213 - Distributed model predictive control for plant-wide systems

Local Cost Optimization Based Distributed Predictive Control with Constraints 187

u 1
0
u 2
u 3
u 4
–0.5
u i

–1

–1.5
5 10 15 20
Time (s)

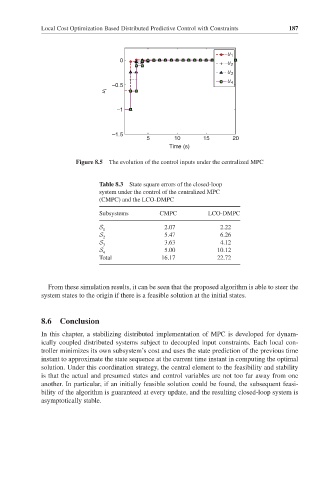
Figure 8.5 The evolution of the control inputs under the centralized MPC

Table 8.3 State square errors of the closed-loop
system under the control of the centralized MPC
(CMPC) and the LCO-DMPC
Subsystems CMPC LCO-DMPC

S 1 2.07 2.22
S 2 5.47 6.26
S 3 3.63 4.12
S 4 5.00 10.12
Total 16.17 22.72

From these simulation results, it can be seen that the proposed algorithm is able to steer the
system states to the origin if there is a feasible solution at the initial states.

8.6 Conclusion

In this chapter, a stabilizing distributed implementation of MPC is developed for dynam-
ically coupled distributed systems subject to decoupled input constraints. Each local con-
troller minimizes its own subsystem’s cost and uses the state prediction of the previous time
instant to approximate the state sequence at the current time instant in computing the optimal
solution. Under this coordination strategy, the central element to the feasibility and stability
is that the actual and presumed states and control variables are not too far away from one
another. In particular, if an initially feasible solution could be found, the subsequent feasi-
bility of the algorithm is guaranteed at every update, and the resulting closed-loop system is
asymptotically stable.