Page 359 - Dust Explosions in the Process Industries

328 Dust Explosions in the Process Industries

Dependent on Independent of condition
condition of of formation
formation

E(#. t)

$ s ’ 8 Wavenumber, (*
$
-k Energy-containing3 z
Largest eddies of 8 eddies $ Universal equilibrium range
permanent character + ’B
&= const. 3-s
Inertial
subrange
ReY>>> I

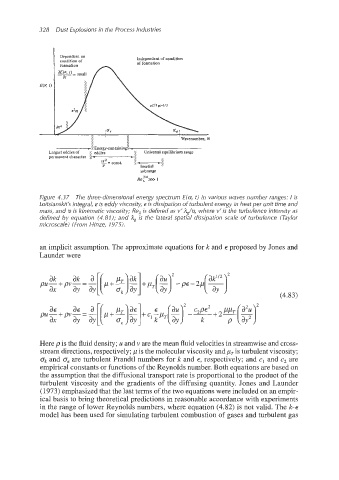
Figure 4.37 The three-dimensional energy spectrum €(a,t) in various waves number ranges: I is
Loitsianskii’s integral, E is eddy viscosity, E is dissipation of turbulent energy in heat per unit time and
mass, and v is kinematic viscosity; Ren is defined as v’ ilg/v, where v’ is the turbulence intensity as
defined by equation (4.81); and ilgis the lateral spatial dissipation scale of turbulence (Taylor
microscale) (From Hinze, 1975).

an implicit assumption. The approximate equations for k and E proposed by Jones and
Launder were

(4.83)
2

Here p is the fluid density; u and v are the mean fluid velocities in streamwiseand cross-
stream directions,respectively;,uis the molecular viscosity and ,uT is turbulent viscosity;
o,and o,are turbulent Prandtl numbers for k and E, respectively; and cI and c2 are
empirical constants or functions of the Reynolds number. Both equations are based on
the assumption that the diffusional transport rate is proportional to the product of the
turbulent viscosity and the gradients of the diffusing quantity. Jones and Launder
(1973) emphasized that the last terms of the two equations were included on an empir-
ical basis to bring theoretical predictions in reasonable accordance with experiments
in the range of lower Reynolds numbers, where equation (4.82) is not valid. The k-E
model has been used for simulating turbulent combustion of gases and turbulent gas