Page 423 - Dust Explosions in the Process Industries

390 Dust Explosions in the Process Industries

the temperature (K). Some further experimental results produced by Leuschke (1980,
1981) are mentioned in Section 5.2.3.2.
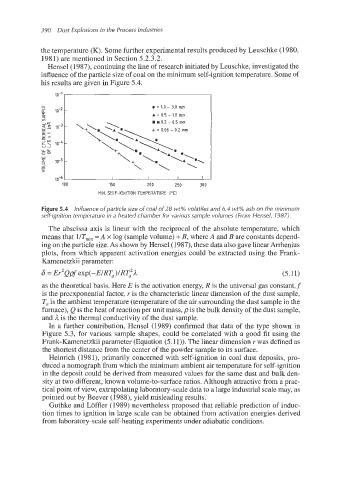
Hensel(1987), continuing the line of research initiated by Leuschke, investigated the
influence of the particle size of coal on the minimum self-ignitiontemperature. Some of
his results are given in Figure 5.4.

.
v) 0.2 - 0.5 rnm
AI7 -
5 E + = 0.06 - 0.2 mm
z.-
2 II
10
I; 10-4-
!g% ++ A '
10-5 -
3 \\ \
0
>
10-6 I I I I I
100 150 200 250 300
MIN. SELF-IGNITION TEMPERATURE I"C1
Figure 5.4 Influence ofparticle size of coal of28 wt% volatiles and 6.4 wt% ash on the minimum
self-ignition temperature in a heated chamber for various sample volumes (From Hensel, 1987).

The abscissa axis is linear with the reciprocal of the absolute temperature, which
means that l/T~n =A x log (sample volume) +B, where A and B are constants depend-
ing on the particle size. As shown by Hensel(1987), these data also gave linearArrhenius
plots, from which apparent activation energies could be extracted using the Frank-
Kamenetzkii parameter:
6 = Er2Qpf exp(-EIRT,)IR<'A (5.11)
as the theoretical basis. Here E is the activation energy, R is the universal gas constant,f
is the preexponential factor, r is the characteristic linear dimension of the dust sample,
T, is the ambient temperature (temperature of the air surroundingthe dust sample in the
furnace), Q is the heat of reaction per unit mass, p is the bulk density of the dust sample,
and ilis the thermal conductivity of the dust sample.
In a further contribution, Hensel (1989) confirmed that data of the type shown in
Figure 5.3, for various sample shapes, could be correlated with a good fit using the
Frank-Kamenetzkiiparameter (Equation (5.11)). The linear dimension r was defined as
the shortest distance from the center of the powder sample to its surface.
Heinrich (19Sl), primarily concerned with self-ignition in coal dust deposits, pro-
duced a nomograph from which the minimum ambient air temperature for self-ignition
in the deposit could be derived from measured values for the same dust and bulk den-
sity at two different, known volume-to-surfaceratios. Although attractive from a prac-
tical point of view, extrapolatinglaboratory-scaledata to a large industrial scale may, as
pointed out by Beever (1988), yield misleading results.
Guthke and Loffler (1989) nevertheless proposed that reliable prediction of induc-
tion times to ignition in large scale can be obtained from activation energies derived
from laboratory-scale self-heating experiments under adiabatic conditions.