Page 27 - Dynamic Loading and Design of Structures

Page 14

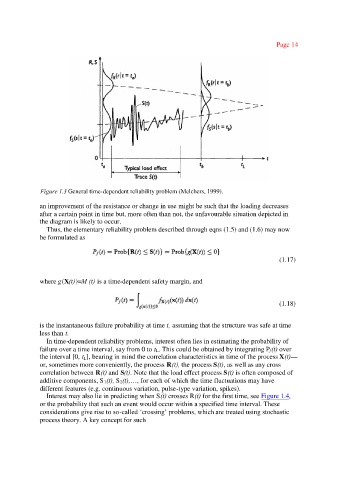
Figure 1.3 General time-dependent reliability problem (Melchers, 1999).

an improvement of the resistance or change in use might be such that the loading decreases
after a certain point in time but, more often than not, the unfavourable situation depicted in
the diagram is likely to occur.
Thus, the elementary reliability problem described through eqns (1.5) and (1.6) may now
be formulated as

(1.17)

where g(X(t))=M (t) is a time-dependent safety margin, and

(1.18)

is the instantaneous failure probability at time t, assuming that the structure was safe at time
less than t.
In time-dependent reliability problems, interest often lies in estimating the probability of
failure over a time interval, say from 0 to tL. This could be obtained by integrating Pf(t) over
the interval [0, t ], bearing in mind the correlation characteristics in time of the process X(t)—
L
or, sometimes more conveniently, the process R(t), the process S(t), as well as any cross
correlation between R(t) and S(t). Note that the load effect process S(t) is often composed of
additive components, S 1(t), S2(t),…, for each of which the time fluctuations may have
different features (e.g. continuous variation, pulse-type variation, spikes).
Interest may also lie in predicting when S(t) crosses R(t) for the first time, see Figure 1.4,
or the probability that such an event would occur within a specified time interval. These
considerations give rise to so-called ‘crossing’ problems, which are treated using stochastic
process theory. A key concept for such