Page 28 - Dynamic Loading and Design of Structures

Page 15

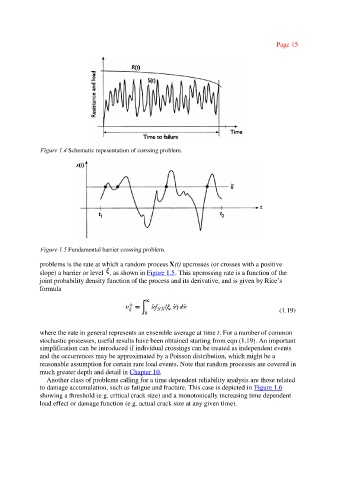
Figure 1.4 Schematic repesentation of corssing problem.

Figure 1.5 Fundamental barrier crossing problem.

problems is the rate at which a random process X(t) upcrosses (or crosses with a positive
slope) a barrier or level , as shown in Figure 1.5. This upcrossing rate is a function of the
joint probability density function of the process and its derivative, and is given by Rice’s
formula

(1.19)

where the rate in general represents an ensemble average at time t. For a number of common
stochastic processes, useful results have been obtained starting from eqn (1.19). An important
simplification can be introduced if individual crossings can be treated as independent events
and the occurrences may be approximated by a Poisson distribution, which might be a
reasonable assumption for certain rare load events. Note that random processes are covered in
much greater depth and detail in Chapter 10.
Another class of problems calling for a time dependent reliability analysis are those related
to damage accumulation, such as fatigue and fracture. This case is depicted in Figure 1.6
showing a threshold (e.g. critical crack size) and a monotonically increasing time dependent
load effect or damage function (e.g. actual crack size at any given time).