Page 47 - Dynamics and Control of Nuclear Reactors

38 CHAPTER 4 Solutions of the point reactor kinetics equations

As demonstrated in Fig. 4.2, there is a significant difference in the response when
ρ < β and when ρ > β. As a result, it has become common to express reactivity as a
fraction of the value when ρ ¼ β. This unit is called a dollar of reactivity. That is, one
dollar of reactivity is numerically equal to the magnitude of total delayed neutron
fraction, β, or 1dollar ($) ¼ β. In general, reactivity (dollars) ¼ ρ/β. Likewise, reac-
tivity in cents is defined as reactivity (cents) ¼ 100 [ρ/β]. Clearly, it is necessary to
limit reactivity inputs to a few cents. In future illustrations in this book, reactivity is
usually expressed in cents.
If there were no delayed neutrons, the kinetics model becomes.
ρ

d P P
¼ (4.7)
dt P 0ðÞ Λ P 0ðÞ
The response in this case is given by.
ρt
P
¼ exp (4.8)
P 0ðÞ Λ
This equation indicates a much greater rate of increase than that seen with a model
that appropriately includes delayed neutrons.
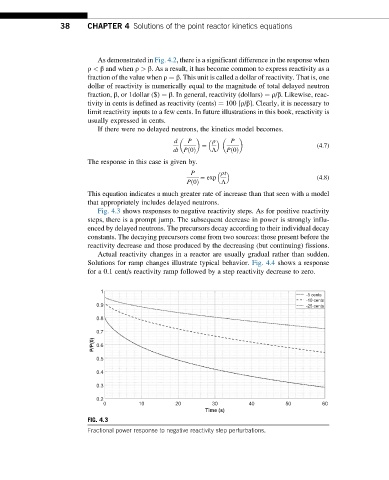
Fig. 4.3 shows responses to negative reactivity steps. As for positive reactivity
steps, there is a prompt jump. The subsequent decrease in power is strongly influ-
enced by delayed neutrons. The precursors decay according to their individual decay
constants. The decaying precursors come from two sources: those present before the
reactivity decrease and those produced by the decreasing (but continuing) fissions.
Actual reactivity changes in a reactor are usually gradual rather than sudden.
Solutions for ramp changes illustrate typical behavior. Fig. 4.4 shows a response
for a 0.1 cent/s reactivity ramp followed by a step reactivity decrease to zero.

1
-5 cents
-10 cents
0.9 -25 cents
0.8
0.7
P/P(0) 0.6

0.5
0.4
0.3

0.2
0 10 20 30 40 50 60
Time (s)
FIG. 4.3
Fractional power response to negative reactivity step perturbations.