Page 122 - Electrical Properties of Materials

104 The band theory of solids

sin αa
P + cos αa
αa

+1
αa
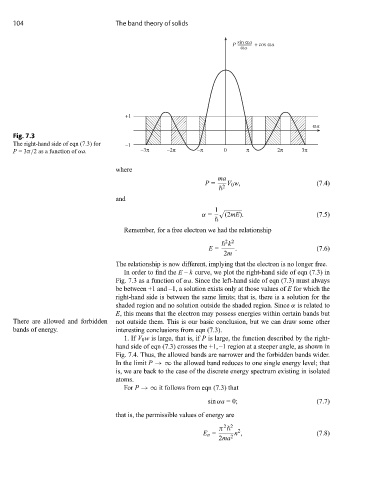
Fig. 7.3
The right-hand side of eqn (7.3) for –1
P =3π/2 as a function of αa. –3π –2π –π 0 π 2π 3π

where
ma
P = V 0 w, (7.4)
2
and
1
α = (2mE). (7.5)

Remember, for a free electron we had the relationship

2 2
k
E = . (7.6)
2m
The relationship is now different, implying that the electron is no longer free.
In order to find the E – k curve, we plot the right-hand side of eqn (7.3) in
Fig. 7.3 as a function of αa. Since the left-hand side of eqn (7.3) must always
be between +1 and –1, a solution exists only at those values of E for which the
right-hand side is between the same limits; that is, there is a solution for the
shaded region and no solution outside the shaded region. Since α is related to
E, this means that the electron may possess energies within certain bands but
There are allowed and forbidden not outside them. This is our basic conclusion, but we can draw some other
bands of energy. interesting conclusions from eqn (7.3).
1. If V 0 w is large, that is, if P is large, the function described by the right-
hand side of eqn (7.3) crosses the +1, –1 region at a steeper angle, as shown in
Fig. 7.4. Thus, the allowed bands are narrower and the forbidden bands wider.
In the limit P →∞ the allowed band reduces to one single energy level; that
is, we are back to the case of the discrete energy spectrum existing in isolated
atoms.
For P →∞ it follows from eqn (7.3) that
sin αa = 0; (7.7)

that is, the permissible values of energy are
2 2
π 2
E n = n , (7.8)
2ma 2