Page 121 - Electrical Properties of Materials

The Kronig–Penney model 103

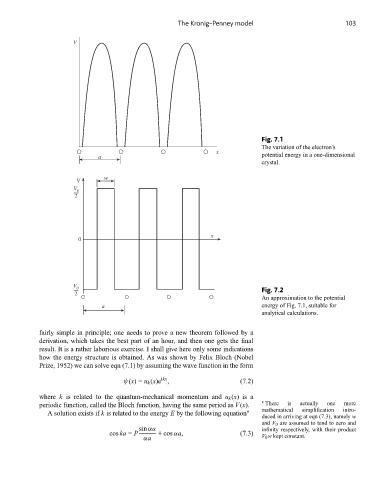
V

Fig. 7.1
The variation of the electron’s
x
a potential energy in a one-dimensional
crystal.

w
V
V
0
2

x
0

V
0 Fig. 7.2
2
An approximation to the potential
a energy of Fig. 7.1, suitable for
analytical calculations.

fairly simple in principle; one needs to prove a new theorem followed by a
derivation, which takes the best part of an hour, and then one gets the final
result. It is a rather laborious exercise. I shall give here only some indications
how the energy structure is obtained. As was shown by Felix Bloch (Nobel
Prize, 1952) we can solve eqn (7.1) by assuming the wave function in the form
ikx
ψ(x)= u k (x)e , (7.2)

where k is related to the quantum-mechanical momentum and u k (x)isa
∗ There is actually one more
periodic function, called the Bloch function, having the same period as V(x). mathematical simplification intro-
A solution exists if k is related to the energy E by the following equation ∗
duced in arriving at eqn (7.3), namely w
and V 0 areassumedtotendtozeroand
sin αa infinity respectively, with their product
cos ka = P + cos αa, (7.3) V 0 w kept constant.
αa