Page 123 - Electrical Properties of Materials

The Kronig–Penney model 105

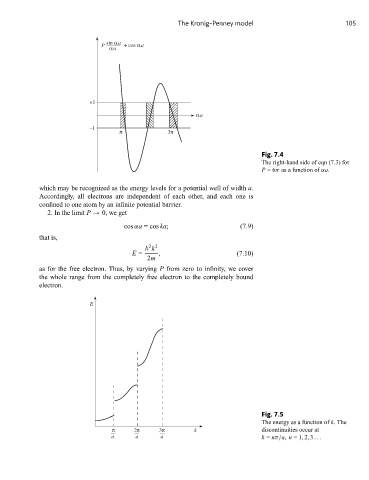
sin αa
P + cos αa
αa

+1
αa

–1
π 3π

Fig. 7.4
The right-hand side of eqn (7.3) for
P =6π as a function of αa.

which may be recognized as the energy levels for a potential well of width a.
Accordingly, all electrons are independent of each other, and each one is
confined to one atom by an infinite potential barrier.
2. In the limit P → 0, we get
cos αa = cos ka; (7.9)

that is,
2 2
k
E = , (7.10)
2m
as for the free electron. Thus, by varying P from zero to infinity, we cover
the whole range from the completely free electron to the completely bound
electron.

E

Fig. 7.5
The energy as a function of k.The
π 2π 3π k discontinuities occur at
a a a k = nπ/a, n =1, 2, 3 ...