Page 303 - Electrical Properties of Materials

The quantum Hall effect 285

You may remember the discussion of the ordinary Hall effect in Chapter 1.
The experimental set-up for the quantum Hall effect is exactly the same. The
only difference is that the dimension of the current channel perpendicular to
the applied magnetic field is now comparable with the electron wavelength.
~
The requirements for observing the effect are high magnetic fields (B = 10 T)
and low temperatures, say a few K. The measured value is the so-called Hall
resistance, which relates the measured transverse voltage (Hall voltage) to the
longitudinal current. Since the Hall voltage is known to be proportional to the Hall resistance
applied magnetic field [eqn (1.20)] we would expect the Hall resistance versus
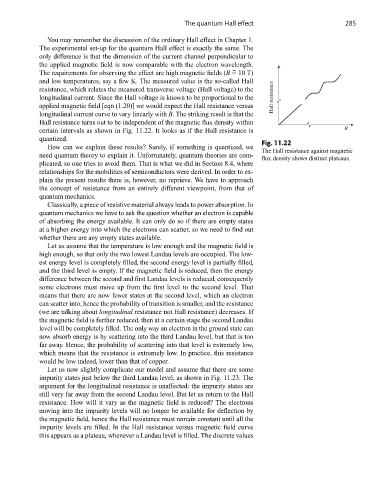
longitudinal current curve to vary linearly with B. The striking result is that the
Hall resistance turns out to be independent of the magnetic flux density within
certain intervals as shown in Fig. 11.22. It looks as if the Hall resistance is B
quantized. Fig. 11.22
How can we explain these results? Surely, if something is quantized, we
The Hall resistance against magnetic
need quantum theory to explain it. Unfortunately, quantum theories are com-
flux density shows distinct plateaus.
plicated, so one tries to avoid them. That is what we did in Section 8.4, where
relationships for the mobilities of semiconductors were derived. In order to ex-
plain the present results there is, however, no reprieve. We have to approach
the concept of resistance from an entirely different viewpoint, from that of
quantum mechanics.
Classically, a piece of resistive material always leads to power absorption. In
quantum mechanics we have to ask the question whether an electron is capable
of absorbing the energy available. It can only do so if there are empty states
at a higher energy into which the electrons can scatter, so we need to find out
whether there are any empty states available.
Let us assume that the temperature is low enough and the magnetic field is
high enough, so that only the two lowest Landau levels are occupied. The low-
est energy level is completely filled, the second energy level is partially filled,
and the third level is empty. If the magnetic field is reduced, then the energy
difference between the second and first Landau levels is reduced, consequently
some electrons must move up from the first level to the second level. That
means that there are now fewer states at the second level, which an electron
can scatter into, hence the probability of transition is smaller, and the resistance
(we are talking about longitudinal resistance not Hall resistance) decreases. If
the magnetic field is further reduced, then at a certain stage the second Landau
level will be completely filled. The only way an electron in the ground state can
now absorb energy is by scattering into the third Landau level, but that is too
far away. Hence, the probability of scattering into that level is extremely low,
which means that the resistance is extremely low. In practice, this resistance
would be low indeed, lower than that of copper.
Let us now slightly complicate our model and assume that there are some
impurity states just below the third Landau level, as shown in Fig. 11.23. The
argument for the longitudinal resistance is unaffected: the impurity states are
still very far away from the second Landau level. But let us return to the Hall
resistance. How will it vary as the magnetic field is reduced? The electrons
moving into the impurity levels will no longer be available for deflection by
the magnetic field, hence the Hall resistance must remain constant until all the
impurity levels are filled. In the Hall resistance versus magnetic field curve
this appears as a plateau, whenever a Landau level is filled. The discrete values