Page 398 - Electrical Properties of Materials

380 Superconductivity

After much labour we have, at last, arrived at a useful relationship. We now
have a theory that connects the independently measurable quantities L, V, H c ,
and T. After measuring them, determining d H c /dT from the H c – T plot, and
substituting their values into eqn (14.32), the equation should be satisfied; and
it is satisfied to a good approximation thus giving us experimental proof that
we are on the right track.
It is interesting to note that L vanishes at two extremes of temperature,
namely, at T = 0 and at T = T c where the critical magnetic field is zero.
A transition which takes place with no latent heat is called a second-order
phase transition. In this transition entropy remains constant, and the specific
heat is discontinuous.
Neglecting the difference between the specific heats at constant volume and
constant pressure, we can write, in general for the specific heat,
dS
c = T . (14.33)
dT
Substituting from eqn (14.30),

dS n dS s
c n – c s = T –
dT dT

2 2
d H c d H c
=–VTμ 0 –H c 2 + . (14.34)
dT dT
At T = T c where H c =0,

2

d H c
c n – c s =– VTμ 0 . (14.35)
d T
T=T c
This is negative because the experimentally established H c – T curves have
finite slopes at T = T c . It follows that in the absence of a magnetic field the

t
a
e
h

c
i
f
i
c
e
p
S
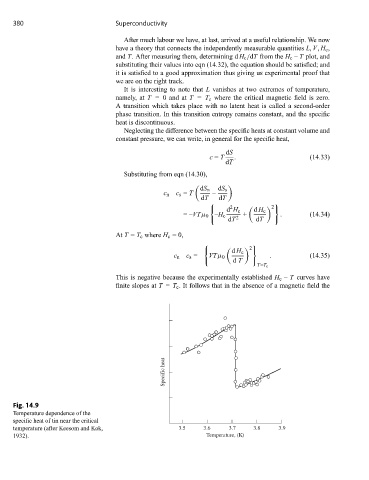
Fig. 14.9
Temperature dependence of the
specific heat of tin near the critical
temperature (after Keesom and Kok, 3.5 3.6 3.7 3.8 3.9
1932). Temperature, (K)