Page 278 - Electromagnetics

0.6

v g

0.4

v/c v p

0.2

0.0
9 10 11 12
log (f)
10
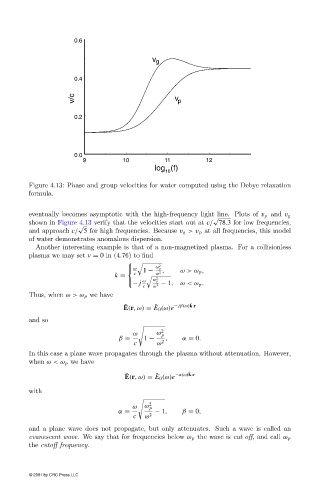
Figure 4.13: Phase and group velocities for water computed using the Debye relaxation
formula.

eventually becomes asymptotic with the high-frequency light line. Plots of v p and v g
√
shown in Figure 4.13 verify that the velocities start out at c/ 78.3 for low frequencies,
√
and approach c/ 5 for high frequencies. Because v g >v p at all frequencies, this model
of water demonstrates anomalous dispersion.
Another interesting example is that of a non-magnetized plasma. For a collisionless
plasma we may set ν = 0 in (4.76) to find

2
 ω ω p
c 1 − ω 2 , ω > ω p ,
k = 2
− j 2 − 1,ω < ω p .
 ω ω p
c ω
Thus, when ω> ω p we have
˜
˜
E(r,ω) = E 0 (ω)e − jβ(ω) ˆ k·r
and so

ω ω 2 p
β = 1 − , α = 0.
c ω 2
In this case a plane wave propagates through the plasma without attenuation. However,
when ω< ω p we have
˜
˜
E(r,ω) = E 0 (ω)e −α(ω) ˆ k·r
with

ω ω 2 p
α = − 1, β = 0,
c ω 2
and a plane wave does not propagate, but only attenuates. Such a wave is called an
evanescent wave. We say that for frequencies below ω p the wave is cut off, and call ω p
the cutoff frequency.

© 2001 by CRC Press LLC