Page 302 - Electromagnetics

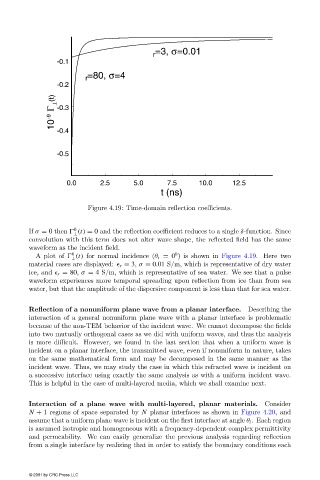
=3, σ=0.01
r
-0.1

=80, σ=4
r
-0.2
10 -9 Γ ⊥ (t) -0.3

-0.4

-0.5

0.0 2.5 5.0 7.5 10.0 12.5
t (ns)

Figure 4.19: Time-domain reflection coefficients.

0
If σ = 0 then (t) = 0 and the reflection coefficient reduces to a single δ-function. Since
⊥
convolution with this term does not alter wave shape, the reflected field has the same
waveform as the incident field.
0
0
A plot of (t) for normal incidence (θ i = 0 ) is shown in Figure 4.19. Here two
⊥
material cases are displayed: r = 3, σ = 0.01 S/m, which is representative of drywater
ice, and r = 80, σ = 4 S/m, which is representative of sea water. We see that a pulse
waveform experiences more temporal spreading upon reflection from ice than from sea
water, but that the amplitude of the dispersive component is less than that for sea water.

Reflection of a nonuniform plane wave from a planar interface. Describing the
interaction of a general nonuniform plane wave with a planar interface is problematic
because of the non-TEM behavior of the incident wave. We cannot decompose the fields
into two mutuallyorthogonal cases as we did with uniform waves, and thus the analysis
is more difficult. However, we found in the last section that when a uniform wave is
incident on a planar interface, the transmitted wave, even if nonuniform in nature, takes
on the same mathematical form and maybe decomposed in the same manner as the
incident wave. Thus, we may studythe case in which this refracted wave is incident on
a successive interface using exactlythe same analysis as with a uniform incident wave.
This is helpful in the case of multi-layered media, which we shall examine next.

Interaction of a plane wave with multi-layered, planar materials. Consider
N + 1 regions of space separated by N planar interfaces as shown in Figure 4.20, and
assume that a uniform plane wave is incident on the first interface at angle θ i . Each region
is assumed isotropic and homogeneous with a frequency-dependent complex permittivity
and permeability. We can easily generalize the previous analysis regarding reflection
from a single interface byrealizing that in order to satisfythe boundaryconditions each

© 2001 by CRC Press LLC