Page 414 - Electromagnetics

1.2
incident field
0.8 waveform
B
Relative amplitude -0.0 B: creeping wave
0.4
A

-0.4

-0.8 A: specular
reflection
-1.2
-0.5 0.0 0.5 1.0 1.5 2.0
t/(2πa/c)

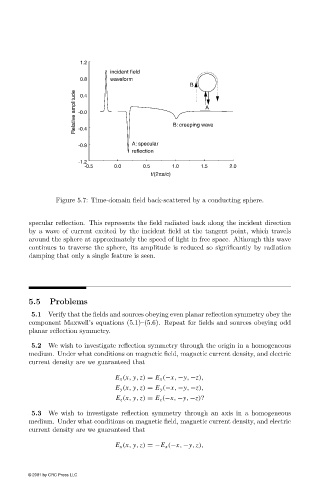
Figure 5.7: Time-domain field back-scattered by a conducting sphere.

specular reflection. This represents the field radiated back along the incident direction
by a wave of current excited by the incident field at the tangent point, which travels
around the sphere at approximately the speed of light in free space. Although this wave
continues to traverse the sphere, its amplitude is reduced so significantly by radiation
damping that only a single feature is seen.

5.5 Problems
5.1 Verify that the fields and sources obeying even planar reflection symmetry obey the
component Maxwell’s equations (5.1)–(5.6). Repeat for fields and sources obeying odd
planar reflection symmetry.
5.2 We wish to investigate reflection symmetry through the origin in a homogeneous
medium. Under what conditions on magnetic field, magnetic current density, and electric
current density are we guaranteed that

E x (x, y, z) = E x (−x, −y, −z),
E y (x, y, z) = E y (−x, −y, −z),
E z (x, y, z) = E z (−x, −y, −z)?
5.3 We wish to investigate reflection symmetry through an axis in a homogeneous
medium. Under what conditions on magnetic field, magnetic current density, and electric
current density are we guaranteed that

E x (x, y, z) =−E x (−x, −y, z),

© 2001 by CRC Press LLC