Page 413 - Electromagnetics

10.00

1.00
σ/πa 2

0.10

0.01
0 1 2 3 4 5 6 7 8 9 10
ka

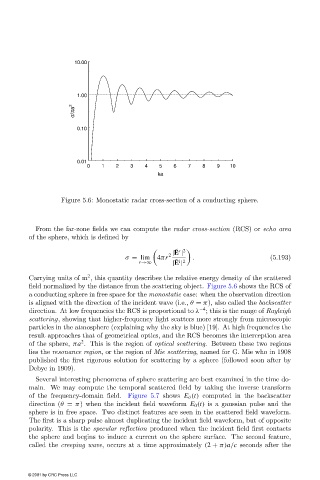
Figure 5.6: Monostatic radar cross-section of a conducting sphere.

From the far-zone fields we can compute the radar cross-section (RCS) or echo area
of the sphere, which is defined by

˜ s 2
|E |
2
σ = lim 4πr . (5.193)
˜ i 2
r→∞ |E |
2
Carrying units of m , this quantity describes the relative energy density of the scattered
field normalized by the distance from the scattering object. Figure 5.6 shows the RCS of
a conducting sphere in free space for the monostatic case: when the observation direction
is aligned with the direction of the incident wave (i.e., θ = π), also called the backscatter
−4
direction. At lowfrequencies the RCS is proportional to λ ; this is the range of Rayleigh
scattering, showing that higher-frequency light scatters more strongly from microscopic
particles in the atmosphere (explaining why the sky is blue) [19]. At high frequencies the
result approaches that of geometrical optics, and the RCS becomes the interception area
2
of the sphere, πa . This is the region of optical scattering. Between these two regions
lies the resonance region, or the region of Mie scattering, named for G. Mie who in 1908
published the first rigorous solution for scattering by a sphere (followed soon after by
Debye in 1909).
Several interesting phenomena of sphere scattering are best examined in the time do-
main. We may compute the temporal scattered field by taking the inverse transform
of the frequency-domain field. Figure 5.7 shows E θ (t) computed in the backscatter
direction (θ = π) when the incident field waveform E 0 (t) is a gaussian pulse and the
sphere is in free space. Two distinct features are seen in the scattered field waveform.
The first is a sharp pulse almost duplicating the incident field waveform, but of opposite
polarity. This is the specular reflection produced when the incident field first contacts
the sphere and begins to induce a current on the sphere surface. The second feature,
called the creeping wave, occurs at a time approximately (2 + π)a/c seconds after the

© 2001 by CRC Press LLC