Page 255 - Elements of Chemical Reaction Engineering 3rd Edition

Sec. 5.1 Batch Reactor Data, 227

Polynomial Fit. Another technique to differentiate the data is to first fit the
concentration-time data to an nth-order polynomial:

C, = a. + a,t + a,t2 + ... f- a,tn (5-1 1)

Many personal computer software packages contain programs that will calcu-
late tlhe best values for the constants ai. One has only to enter th., concentra-
n
tion-time data and choose the order of the polynomial. After determining the
constants, ai, one has only to differentiate Equation (5-11) with respect to time:

(5-12)

Thus concentration and the time rate of change of concentration are both
known at any time t.
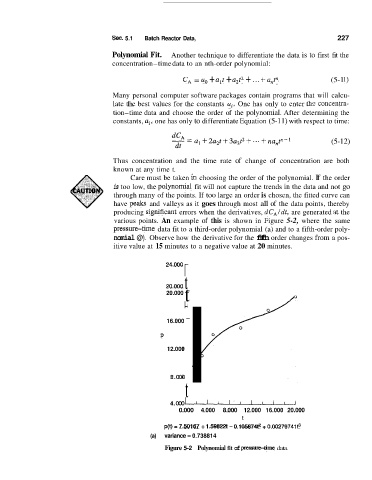
Care must be taken in choosing the order of the polynomial. If the order
is too low, the ]polynomial fit will not capture the trends in the data and not go
through many of the points. If too large an order is chosen, the fitted curve can
have peaks and valleys as it goes through most all of the data points, thereby
producing signjficant errors when the derivatives, dCA/dt, are generated iit the
various points. An example of this is shown in Figure 5-2, where the same
pressuretime data fit to a third-order polynomial (a) and to a fifth-order poly-
nomial @). Observe how the derivative for the fifth order changes from a pos-
itive value at 15 minutes to a negative value at 20 minutes.

t

-
I
20.000
20.000 t P
L -
16.000 -
16.000
P P
12.000

8.000
t

4.000 3
0.000 4.000 8.000 12.000 16.000 20.000
t
p(t) = 7.50167 + 1.59822t - 0.1056746 + 0.00279741@
(a) variance = 0.738814
Figure 5-2 Polynomial fit of pressuretime data.