Page 343 - Elements of Chemical Reaction Engineering Ebook

314 Multiple Reactions Chap. 6

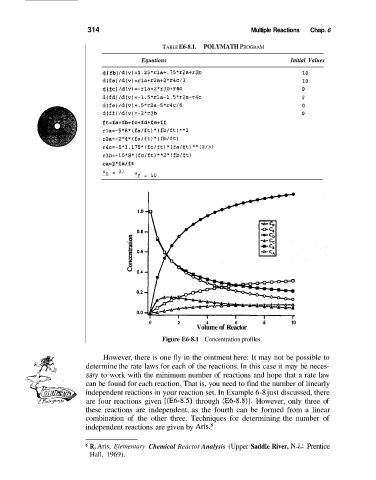
TABLE E6-8.1. POLYMATH PROGRAM
Equations Initial Values
d( fb) /d(v)=l.25*rla+. 75*rZa+r3b 10
d(fa)/d(v)=rla+r2a+2*r4~/3 10
d(fc) /d(v)=-rla+2*r3btr4c 0
d(fd)/d(v)=-1.5*rla-l.5*rZa-r4c 0
d(fe)/d(v)=.5*r2a-5*r4~/6 0
d(ff)/d(v)=-2*r3b 0
ft=fa+fb+fc+fd+fe+ff
rla=-S*e*(fa/ft)*(fb/ft)**2
rZa=-2*4*(fa/ft)*(fb/ft)
r4~=-5*3.175*(fc/ft)*(fa/ft)**(2/3)
r3b=-10*8*(fc/ft)**2*[fb/ft)
ca=2*fa/ft
v* = 0, Vf = 10

0 2 4 6 a 10
Volume of Reactor
Figure E6-8.1 Concentration profiles.

However, there is one fly in the ointment here: It may not be possible to
determine the rate laws for each of the reactions. In this case it may be neces-
sary to work with the minimum number of reactions and hope that a rate law
can be found for each reaction. That is, you need to find the number of linearly
independent reactions in your reaction set. In Example 6-8 just discussed, there
are four reactions given [(E6-8:5) through (E6-8.8)]. However, only three of
these reactions are independent, as the fourth can be formed from a linear
combination of the other three. Techniques for determining the number of
independent reactions are given by Ark8

R. Ark, Elementaly Chemical Reactor Analysis (Upper Saddle River, N.J; Prentice
Hall, 1969).