Page 74 - Elements of Chemical Reaction Engineering Ebook

Sec. 2 3 Applications of the Design Equations for Continuous-Flow Reactors 45

0.2 0.4 0.6 0.8

Conversion, X
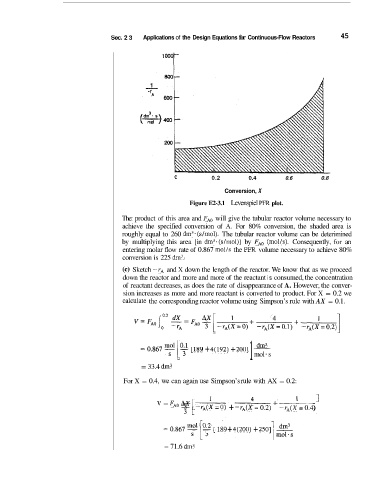
Figure E2-3.1 Levenspiel PFR plot.

The: product of this area and FAO will give the tubular reactor volume necessary to
achieve the specified conversion of A. For 80% conversion, the shaded area is
roughly equal to 260 dm3*(s/mol). The tubular reactor volume can be deterimined
by multiplying this area [in dm3.(s/mol)] by FA,, (mol/s). Consequently, for an
entering molar flow rate of 0.867 mol/s the PFR volume necessary to achieve 80%
conversion is 225 dm3.
(c) Sketch -rA and X down the length of the reactor. We know that as we proceed
down the reactor and more and more of the reactant is consumed, the concentration
of reactant decreases, as does the rate of disappearance of A. However, the conver-
sion increases as more and more reactant is converted to product. For X = 0.2 we
cak!ulate the corresponding reactor volume using Simpson’s rule with AX = 0.1.

[I89 + 4(192) + 2001 ~
mol * s
L 1 dm3
= 33.4 dm3
For X = 0.4, we can again use Simpson’s rule with AX = 0.2:

v = FAO - 4 +
3
“I -rA(x = 0) + -TA(X = 0.2) -rA(X = 0.4)
L
0.2 { 189 + 4(200) + 2.501

= 71.6 dm3