Page 165 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: LLL Final
Encyclopedia of Physical Science and Technology EN003H-565 June 13, 2001 20:37

Coherent Control of Chemical Reactions 227

We note that the lowest adiabatic state, Eq. (58), is ex-
pressed in terms of the initial and the final states without
the intermediate state. This property implies that the sys-
tem in the initial state is transferred to the final state adia-
batically, with no population in the intermediate resonant
state. That is, under the condition for the Rabi frequencies
| P (t)| | S (t)|, we can see from Eqs. (64) and (65)
that ψ 0 (0) = φ 1 and ψ 0 (∞) = φ 3 if the Stokes pulse comes
before the pump pulse. The ordering of these pulses in
STIRAP is counterintuitive, compared with conventional,
stimulated Raman scattering processes. Figure 23 shows
the time evolution of the Rabi frequencies, mixing angle,
dressed-state eigenvalues, and the population of the ini-
tial and final levels. The counterintuitive pulse sequence
is evident in Figure 23a. One of the properties of STIRAP

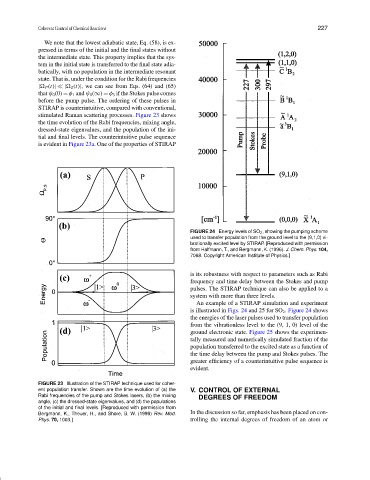
FIGURE 24 Energy levels of SO 2 , showing the pumping scheme
used to transfer population from the ground level to the (9,1,0) vi-
brationally excited level by STIRAP. [Reproduced with permission
from Halfmann, T., and Bergmann, K. (1996). J. Chem. Phys. 104,
7068. Copyright American Institute of Physics.]

is its robustness with respect to parameters such as Rabi
frequency and time delay between the Stokes and pump
pulses. The STIRAP technique can also be applied to a
system with more than three levels.
An example of a STIRAP simulation and experiment
is illustrated in Figs. 24 and 25 for SO 2 . Figure 24 shows
the energies of the laser pulses used to transfer population
from the vibrationless level to the (9, 1, 0) level of the
ground electronic state. Figure 25 shows the experimen-
tally measured and numerically simulated fraction of the
population transferred to the excited state as a function of
the time delay between the pump and Stokes pulses. The
greater efficiency of a counterintuitive pulse sequence is
evident.

FIGURE 23 Illustration of the STIRAP technique used for coher-
ent population transfer. Shown are the time evolution of (a) the V. CONTROL OF EXTERNAL
Rabi frequencies of the pump and Stokes lasers, (b) the mixing DEGREES OF FREEDOM
angle, (c) the dressed-state eigenvalues, and (d) the populations
of the initial and final levels. [Reproduced with permission from
Bergmann, K., Theuer, H., and Shore, B. W. (1998) Rev. Mod. In the discussion so far, emphasis has been placed on con-
Phys. 70, 1003.] trolling the internal degrees of freedom of an atom or