Page 160 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: LLL Final
Encyclopedia of Physical Science and Technology EN003H-565 June 13, 2001 20:37

222 Coherent Control of Chemical Reactions

is to solve an inverse problem for the path in a functional
space of J. There are two essential points in the local op-
timization method. The first is to divide the time interval
t f from the initial time into infinitesimally short time in-
tervals. The second point is to impose the final condition
at the end of each time interval, i.e., |ξ(t) = W|ψ(t) .
Following this procedure, the optimized pulse at time t is
expressed as
ε(t) =−2A(t)Im
ψ(t)|Wµ|ψ(t) . (47)
The simplest method for obtaining this expression is
to substitute Eq. (46) into Eq. (44) after changing t f to t
in Eq. (46). This means that a (virtual) target is set just
after each infinitesimally small time increment, and then
the virtual target is moved toward the final true target po-
sition. The necessary condition for local optimization is
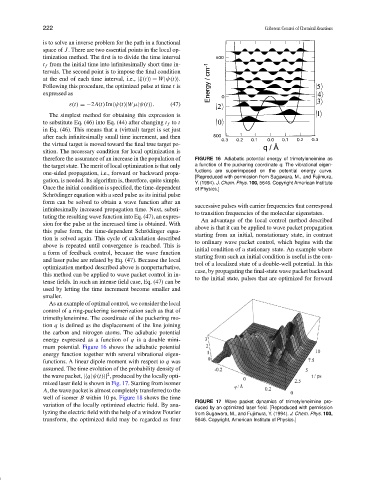
therefore the assurance of an increase in the population of FIGURE 16 Adiabatic potential energy of trimetyleneimine as
the target state. The merit of local optimization is that only a function of the puckering coordinate q. The vibrational eigen-
fuctions are superimposed on the potential energy curve.
one-sided propagation, i.e., forward or backward propa-
[Reproduced with permission from Sugawara, M., and Fujimura,
gation, is needed. Its algorithm is, therefore, quite simple.
Y. (1994). J. Chem. Phys. 100, 5646. Copyright American Institute
Once the initial condition is specified, the time-dependent of Physics.]
Schr¨odinger equation with a seed pulse as its initial pulse
form can be solved to obtain a wave function after an
successive pulses with carrier frequencies that correspond
infinitesimally increased propagation time. Next, substi-
to transition frequencies of the molecular eigenstates.
tuting the resulting wave function into Eq. (47), an expres-
An advantage of the local control method described
sion for the pulse at the increased time is obtained. With
above is that it can be applied to wave packet propagation
this pulse form, the time-dependent Schr¨odinger equa-
starting from an initial, nonstationary state, in contrast
tion is solved again. This cycle of calculation described
to ordinary wave packet control, which begins with the
above is repeated until convergence is reached. This is
initial condition of a stationary state. An example where
a form of feedback control, because the wave function
starting from such an initial condition is useful is the con-
and laser pulse are related by Eq. (47). Because the local
trol of a localized state of a double-well potential. In this
optimization method described above is nonperturbative,
case, by propagating the final-state wave packet backward
this method can be applied to wave packet control in in-
to the initial state, pulses that are optimized for forward
tense fields. In such an intense field case, Eq. (47) can be
used by letting the time increment become smaller and
smaller.
As an example of optimal control, we consider the local
control of a ring-puckering isomerization such as that of
trimethyleneimine. The coordinate of the puckering mo-
tion q is defined as the displacement of the line joining
the carbon and nitrogen atoms. The adiabatic potential
energy expressed as a function of q is a double mini-
mum potential. Figure 16 shows the adiabatic potential
energy function together with several vibrational eigen-
functions. A linear dipole moment with respect to q was
assumed. The time evolution of the probability density of
2
the wave packet, |
q |ψ(t) | , produced by the locally opti-
mized laser field is shown in Fig. 17. Starting from isomer
A, the wave packet is almost completely transferred to the
well of isomer B within 10 ps. Figure 18 shows the time
FIGURE 17 Wave packet dynamics of trimetyleneimine pro-
variation of the locally optimized electric field. By ana-
duced by an optimized laser field. [Reproduced with permission
lyzing the electric field with the help of a window Fourier from Sugawara, M., and Fujimura, Y. (1994). J. Chem. Phys. 100,
transform, the optimized field may be regarded as four 5646. Copyright, American Institute of Physics.]