Page 199 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: GAE/LSK P2: FLV Final Pages
Encyclopedia of Physical Science and Technology EN004D-ID159 June 8, 2001 15:47

96 Crystallization Processes

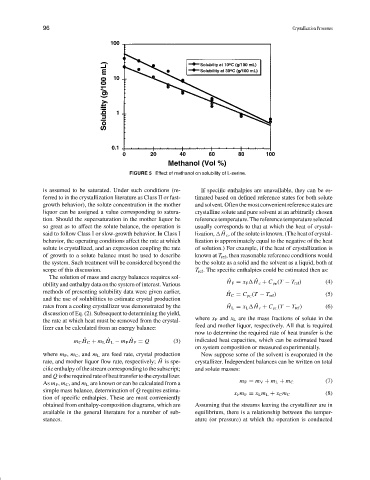
FIGURE 5 Effect of methanol on solubility of L-serine.

is assumed to be saturated. Under such conditions (re- If specific enthalpies are unavailable, they can be es-
ferred to in the crystallization literature as Class II or fast- timated based on defined reference states for both solute
growth behavior), the solute concentration in the mother and solvent. Often the most convenient reference states are
liquor can be assigned a value corresponding to satura- crystalline solute and pure solvent at an arbitrarily chosen
tion. Should the supersaturation in the mother liquor be reference temperature. The reference temperature selected
so great as to affect the solute balance, the operation is usually corresponds to that at which the heat of crystal-
ˆ
said to follow Class I or slow-growth behavior. In Class I lization, H c , of the solute is known. (The heat of crystal-
behavior, the operating conditions affect the rate at which lization is approximately equal to the negative of the heat
solute is crystallized, and an expression coupling the rate of solution.) For example, if the heat of crystallization is
of growth to a solute balance must be used to describe known at T ref , then reasonable reference conditions would
the system. Such treatment will be considered beyond the be the solute as a solid and the solvent as a liquid, both at
scope of this discussion. T ref . The specific enthalpies could be estimated then as:
The solution of mass and energy balances requires sol-
ˆ ˆ (T − T ref ) (4)
ubility and enthalpy data on the system of interest. Various H F = x F H c + C p F
methods of presenting solubility data were given earlier, ˆ
H C = C p C (T − T ref ) (5)
and the use of solubilities to estimate crystal production
rates from a cooling crystallizer was demonstrated by the ˆ ˆ (T − T ref ) (6)
H L = x L H c + C p L
discussion of Eq. (2). Subsequent to determining the yield,
where x F and x L are the mass fractions of solute in the
the rate at which heat must be removed from the crystal-
feed and mother liquor, respectively. All that is required
lizer can be calculated from an energy balance:
now to determine the required rate of heat transfer is the
ˆ
ˆ
ˆ
m C H C + m L H L − m F H F = Q (3) indicated heat capacities, which can be estimated based
on system composition or measured experimentally.
where m F , m C , and m L are feed rate, crystal production Now suppose some of the solvent is evaporated in the
ˆ
rate, and mother liquor flow rate, respectively; H is spe- crystallizer. Independent balances can be written on total
cific enthalpy of the stream corresponding to the subscript; and solute masses:
and Q istherequiredrateofheattransfertothecrystallizer.
(7)
As m F , m C , and m L are known or can be calculated from a m F = m V + m L + m C
simple mass balance, determination of Q requires estima-
x F m F = x L m L + x C m C (8)
tion of specific enthalpies. These are most conveniently
obtained from enthalpy-composition diagrams, which are Assuming that the streams leaving the crystallizer are in
available in the general literature for a number of sub- equilibrium, there is a relationship between the temper-
stances. ature (or pressure) at which the operation is conducted