Page 196 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: GAE/LSK P2: FLV Final Pages
Encyclopedia of Physical Science and Technology EN004D-ID159 June 8, 2001 15:47

Crystallization Processes 93

extensive discussion of the subject matter can be found in conditions and the limitations placed on the operation by
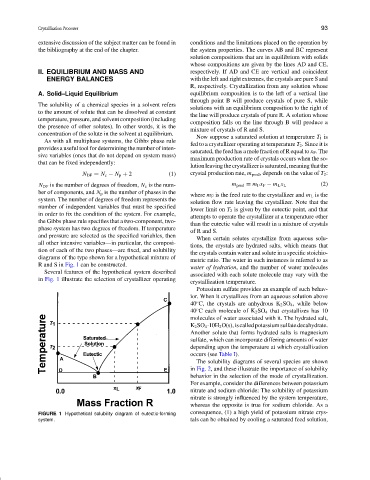
the bibliography at the end of the chapter. the system properties. The curves AB and BC represent
solution compositions that are in equilibrium with solids
whose compositions are given by the lines AD and CE,
II. EQUILIBRIUM AND MASS AND respectively. If AD and CE are vertical and coincident
ENERGY BALANCES with the left and right extremes, the crystals are pure S and
R, respectively. Crystallization from any solution whose
A. Solid–Liquid Equilibrium equilibrium composition is to the left of a vertical line
through point B will produce crystals of pure S, while
The solubility of a chemical species in a solvent refers
solutions with an equilibrium composition to the right of
to the amount of solute that can be dissolved at constant
the line will produce crystals of pure R. A solution whose
temperature, pressure, and solvent composition (including
composition falls on the line through B will produce a
the presence of other solutes). In other words, it is the
mixture of crystals of R and S.
concentration of the solute in the solvent at equilibrium.
Now suppose a saturated solution at temperature T 1 is
As with all multiphase systems, the Gibbs phase rule
fed to a crystallizer operating at temperature T 2 . Since it is
provides a useful tool for determining the number of inten-
saturated, the feed has a mole fraction of R equal to x F . The
sive variables (ones that do not depend on system mass)
maximum production rate of crystals occurs when the so-
that can be fixed independently:
lutionleavingthecrystallizerissaturated,meaningthatthe
N DF = N c − N p + 2 (1) crystal production rate, m prod , depends on the value of T 2 :
N DF is the number of degrees of freedom, N c is the num- m prod = m F x F − m L x L (2)
ber of components, and N p is the number of phases in the
where m F is the feed rate to the crystallizer and m L is the
system. The number of degrees of freedom represents the
solution flow rate leaving the crystallizer. Note that the
number of independent variables that must be specified
lower limit on T 2 is given by the eutectic point, and that
in order to fix the condition of the system. For example,
attempts to operate the crystallizer at a temperature other
the Gibbs phase rule specifies that a two-component, two-
than the eutectic value will result in a mixture of crystals
phase system has two degrees of freedom. If temperature
of R and S.
and pressure are selected as the specified variables, then
When certain solutes crystallize from aqueous solu-
all other intensive variables—in particular, the composi-
tions, the crystals are hydrated salts, which means that
tion of each of the two phases—are fixed, and solubility
the crystals contain water and solute in a specific stoichio-
diagrams of the type shown for a hypothetical mixture of
metric ratio. The water in such instances is referred to as
R and S in Fig. 1 can be constructed.
water of hydration, and the number of water molecules
Several features of the hypothetical system described
associated with each solute molecule may vary with the
in Fig. 1 illustrate the selection of crystallizer operating
crystallization temperature.
Potassium sulfate provides an example of such behav-
ior. When it crystallizes from an aqueous solution above
◦
40 C, the crystals are anhydrous K 2 SO 4 , while below
◦
40 C each molecule of K 2 SO 4 that crystallizes has 10
molecules of water associated with it. The hydrated salt,
K 2 SO 4 ·10H 2 O(s),iscalledpotassiumsulfatedecahydrate.
Another solute that forms hydrated salts is magnesium
sulfate, which can incorporate differing amounts of water
depending upon the temperature at which crystallization
occurs (see Table I).
The solubility diagrams of several species are shown
in Fig. 2, and these illustrate the importance of solubility
behavior in the selection of the mode of crystallization.
For example, consider the differences between potassium
nitrate and sodium chloride: The solubility of potassium
nitrate is strongly influenced by the system temperature,
whereas the opposite is true for sodium chloride. As a
FIGURE 1 Hypothetical solubility diagram of eutectic-forming consequence, (1) a high yield of potassium nitrate crys-
system. tals can be obtained by cooling a saturated feed solution,