Page 349 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: GLQ Final Pages
Encyclopedia of Physical Science and Technology EN009K-419 July 19, 2001 20:57

284 Membranes, Synthetic, Applications

pore allow calculation of transport hindrance of the solute
based on properties of the solvent. For dilute solute con-
centrations, the solvent flows with a well-defined velocity
profile and average velocity that is characteristic of the
pore cross-sectional shape. The solute, on the other hand,
moves with its own characteristic velocity relative to the
pore wall and is assumed to sample all radial positions
available to it during its transport. An expression relat-
ing the local steady state solute flux to a diffusive driving
force and a convective bulk flow term is averaged across
the pore cross section. This procedure yields the steady
state solute flux in terms of the cross sectionally averaged
solute concentration and solvent velocity along the length
of the pore.
Effectively, the theory results in the addition of two
cross-sectionally averaged intrapore hydrodynamic hin-
drance coefficients for diffusion and convection, respec-
tively. Solute hindrance, and hence rejection, relative to
the solvent, increases qualitatively with increasing total
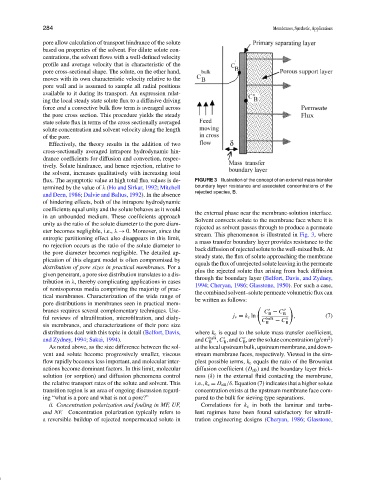
flux. The asymptotic value at high total flux values is de- FIGURE 3 Illustration of the concept of an external mass transfer
termined by the value of λ (Ho and Sirkar, 1992; Mitchell boundary layer resistance and associated concentrations of the
rejected species, B.
and Deen, 1986; Dalvie and Baltus, 1992). In the absence
of hindering effects, both of the intrapore hydrodynamic
coefficients equal unity and the solute behaves as it would
the external phase near the membrane-solution interface.
in an unbounded medium. These coefficients approach
Solvent convects solute to the membrane face where it is
unity as the ratio of the solute diameter to the pore diam-
rejected as solvent passes through to produce a permeate
eter becomes negligible, i.e., λ → 0. Moreover, since the
stream. This phenomenon is illustrated in Fig. 3, where
entropic partitioning effect also disappears in this limit,
a mass transfer boundary layer provides resistance to the
no rejection occurs as the ratio of the solute diameter to
back diffusion of rejected solute to the well-mixed bulk. At
the pore diameter becomes negligible. The detailed ap-
steady state, the flux of solute approaching the membrane
plication of this elegant model is often compromised by
equals the flux of unrejected solute leaving in the permeate
distribution of pore sizes in practical membranes. For a
plus the rejected solute flux arising from back diffusion
given penetrant, a pore size distribution translates to a dis-
through the boundary layer (Belfort, Davis, and Zydney,
tribution in λ, thereby complicating applications in cases
1994; Cheryan, 1986; Glasstone, 1950). For such a case,
of nonisoporous media comprising the majority of prac-
the combined solvent–solute permeate volumetric flux can
tical membranes. Characterization of the wide range of
be written as follows:
pore distributions in membranes seen in practical mem-

branes requires several complementary techniques. Use- C − C B

B
j v = k c ln , (7)
ful reviews of ultrafiltration, microfiltration, and dialy- C B bulk − C B
sis membranes, and characterizations of their pore size
distributions deal with this topic in detail (Belfort, Davis, where k c is equal to the solute mass transfer coefficient,
2

and Zydney, 1994; Sakai, 1994). andC bulk ,C , andC , are the solute concentration (g/cm )
B B B
As noted above, as the size difference between the sol- atthelocalupstreambulk,upstreammembrane,anddown-
vent and solute become progressively smaller, viscous stream membrane faces, respectively. Viewed in the sim-
flow rapidly becomes less important, and molecular inter- plest possible terms, k c equals the ratio of the Brownian
actions become dominant factors. In this limit, molecular diffusion coefficient (D eB ) and the boundary layer thick-
solution (or sorption) and diffusion phenomena control ness (δ) in the external fluid contacting the membrane,
the relative transport rates of the solute and solvent. This i.e., k c = D eB /δ. Equation (7) indicates that a higher solute
transition region is an area of ongoing discussion regard- concentration exists at the upstream membrane face com-
ing “what is a pore and what is not a pore?” pared to the bulk for sieving type separations.
ii. Concentration polarization and fouling in MF, UF, Correlations for k c in both the laminar and turbu-
and NF. Concentration polarization typically refers to lent regimes have been found satisfactory for ultrafil-
a reversible buildup of rejected nonpermeated solute in tration engineering designs (Cheryan, 1986; Glasstone,