Page 312 - Academic Press Encyclopedia of Physical Science and Technology 3rd Polymer

P1: GQT/MBQ P2: GPJ Final Pages
Encyclopedia of Physical Science and Technology EN014C-660 July 28, 2001 17:14

250 Rheology of Polymeric Liquids

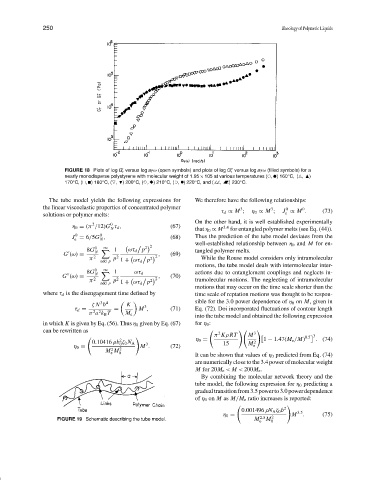
FIGURE 18 Plots of log G versus log a T ω (open symbols) and plots of log G versus log a T ω (filled symbols) for a

r r
◦
nearly monodisperse polystyrene with molecular weight of 1.95 × 105 at various temperatures ( , ) 160 C, ( , )
◦
170 C, ( , ) 180 C, ( , ) 200 C, ( , ) 210 C, ( , ) 220 C, and ( , ) 230 C.
◦
◦
◦
◦
◦
The tube model yields the following expressions for We therefore have the following relationships:
the linear viscoelastic properties of concentrated polymer 3 3 0 0
τ d ∝ M ; η 0 ∝ M ; J ∝ M . (73)
solutions or polymer melts: e
On the other hand, it is well established experimentally
2 0
η 0 = (π /12)G τ d , (67) 3.4
N that η 0 ∝ M for entangled polymer melts (see Eq. (44)).
0 0
J = 6/5G , (68) Thus the prediction of the tube model deviates from the
e N
well-established relationship between η 0 and M for en-
2
∞

8G 0
1 ωτ d p 2 tangled polymer melts.
N
G (ω) = 2 2 , (69)
2
π p 2 While the Rouse model considers only intramolecular
odd p 1 + ωτ d p
motions, the tube model deals with intermolecular inter-
8G 0
1 ωτ d actions due to entanglement couplings and neglects in-
∞
N
G (ω) = , (70)
2
π 2 p 2 1 + ωτ d p 2 tramolecular motions. The neglecting of intramolecular

odd p
motions that may occur on the time scale shorter than the
where τ d is the disengagement time defined by time scale of reptation motions was thought to be respon-
sible for the 3.0 power dependence of η 0 on M, given in
3 4
ζ N b K 3

τ d = = M , (71) Eq. (72). Doi incorporated fluctuations of contour length
2 2
π a k B T M e
into the tube model and obtained the following expression
in which K is given by Eq. (56). Thus η 0 given by Eq. (67) for η 0 :
can be rewritten as 2 3
π KρRT M

0.5 3
2 η 0 = 1 − 1.47(M e /M) . (74)
0.10416 ρb ζ 0 N A 3 15 M 2
0
η 0 = 2 M . (72) e
2
M M 0
e
It can be shown that values of η 0 predicted from Eq. (74)
are numerically close to the 3.4 power of molecular weight
M for 20M e < M < 200M e .
By combining the molecular network theory and the
tube model, the following expression for η 0 predicting a
gradualtransitionfrom3.5powerto3.0powerdependence
of η 0 on M as M/M e ratio increases is reported:
2
0.001496 ρN A ζ 0 b 3.5
η 0 = M . (75)
FIGURE 19 Schematic describing the tube model. M 2.5 M 2
e 0