Page 264 - Engineered Interfaces in Fiber Reinforced Composites

Chapter 6. Interface mechanics and fracture toughness theories 245

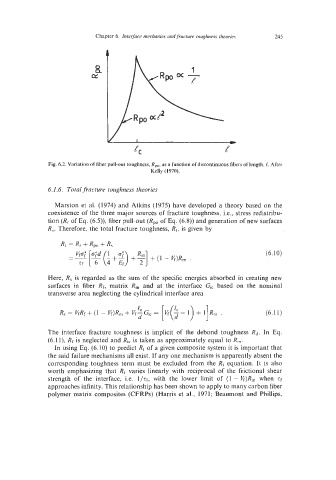
Fig. 6.2. Variation of fiber pull-out toughness, R,, as a function of discontinuous fibers of length, e. After
Kelly (1970).

6.1.6, Total.fracture toughness theories

Marston et al. (1974) and Atkins (1975) have developed a theory based on the
coexistence of the three major sources of fracture toughness, i.e., stress redistribu-
tion (R, of Eq. (6.5)), fiber pull-out (Rpo of Eq. (6.8)) and generation of new surfaces
R,. Therefore, the total fracture toughness, Rt, is given by

(6.10)

Here, R, is regarded as the sum of the specific energies absorbed in creating new
surfaces in fiber Rf, matrix R, and at the interface Gi, based on the nominal
transverse area neglecting the cylindrical interface area

(6.1 1)

The interface fracture toughness is implicit of the debond toughness Rd. In Eq.
(6.1 l), Rf is neglected and Ri, is taken as approximately equal to R,.
In using Eq. (6.10) to predict Rt of a given composite system it is important that
the said failure mechanisms all exist. If any one mechanism is apparently absent the
corresponding toughness term must be excluded from the Rt equation. It is also
worth emphasizing that Rt varies linearly with reciprocal of the frictional shear
strength of the interface, i.e. l/q, with the lower limit of (1 - &)Rm when tr
approaches infinity. This relationship has been shown to apply to many carbon fiber
polymer matrix composites (CFRPs) (Harris et al., 1971; Beaumont and Phillips,