Page 177 - Engineering Digital Design

148 CHAPTER 4/LOGIC FUNCTION REPRESENTATION AND MINIMIZATION

(A+B+D)
C
AB \ 00 \ 01 ' 11 10 AB \ 00 01 ' 11 10 (B+C)

(A+C)

_ _ POS
(A+B+C+D)

BC

AB\ 00 \01 ' 11 10
n
00 0 > 1 3 2

01 w 1
^ 4 5 7 6
CD
11 1 (1 1)
2 13 15 ^S^ 14
A
10 r , ABC
JL_J 1 9 11 10
'SOP
D

(C)
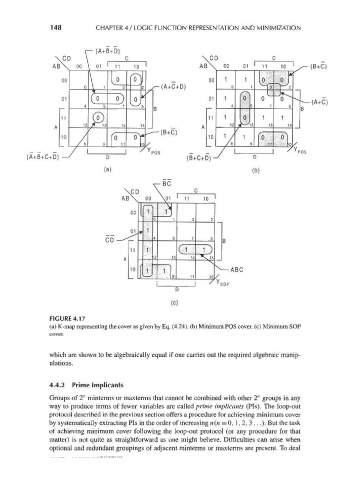
FIGURE 4.17
(a) K-map representing the cover as given by Eq. (4.24). (b) Minimum POS cover, (c) Minimum SOP

which are shown to be algebraically equal if one carries out the required algebraic manip-
ulations.

4.4.2 Prime Implicants
Groups of 2" minterms or maxterms that cannot be combined with other 2" groups in any
way to produce terms of fewer variables are called prime implicants (Pis). The loop-out
protocol described in the previous section offers a procedure for achieving minimum cover
by systematically extracting Pis in the order of increasing n(n = 0, 1,2,3...). But the task
of achieving minimum cover following the loop-out protocol (or any procedure for that
matter) is not quite as straightforward as one might believe. Difficulties can arise when
optional and redundant groupings of adjacent minterms or maxterms are present. To deal