Page 173 - Engineering Digital Design

144 CHAPTER 4/LOGIC FUNCTION REPRESENTATION AND MINIMIZATION

All that is BD
CD C \CD C
AB\ 00 01\' Ti 10 ' - - AB\ 00 / 01 I 11 10
ACD _
All that
00 0 00
is ABC
01 0 1 01
B
11 11 0
12 13 15 14 12 13 15 14
A A
-ABCD
10 10 N 1
11 L L Xal <K9l 11!
7 F SOP
--- / - D All that is CD —f D
-J CD-
BCD -J
(a) (b)
\CD C
AB\ 00 01 ' 11 10 '

00 0 w,
BCD = (B+C+D)- \ 1 2
All that is
01' /~~ NOT ABC = (ABC)
fol
4 5 7 6 / g =A+B+C
Jf
11 0 (o 0
V_x^2 13 15 14
10 fo)
8 9 J In 10 /
I ^
D \ N
— NOT B
(c)
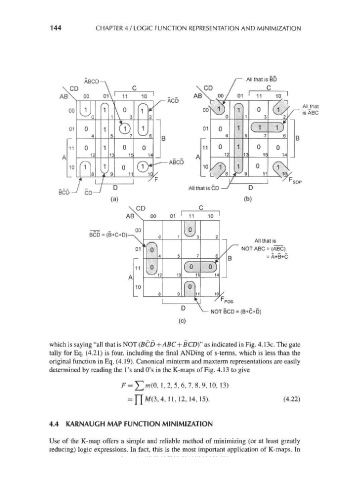
FIGURE 4.13
(a) K-map for the reduced SOP function in Eq. (4.19). (b) K-map showing minimum SOP cover for
the function F. (c) K-map showing minimum POS cover for the function F.

which is saying "all that is NOT (BCD +ABC + BCD)" as indicated in Fig. 4.13c. The gate
tally for Eq. (4.21) is four, including the final ANDing of s-terms, which is less than the
original function in Eq. (4.19). Canonical minterm and maxterm representations are easily
determined by reading the 1's and O's in the K-maps of Fig. 4.13 to give

F = ]Tm(0, 1, 2, 5, 6, 7, 8, 9, 10, 13)
= ]~]M(3,4, 11,12, 14, 15). (4.22)

4.4 KARNAUGH MAP FUNCTION MINIMIZATION

Use of the K-map offers a simple and reliable method of minimizing (or at least greatly
reducing) logic expressions. In fact, this is the most important application of K-maps. In