Page 203 - Engineering Digital Design

174 CHAPTER 4 / LOGIC FUNCTION REPRESENTATION AND MINIMIZATION

CD C \CD
AB\ 00 01 '1 1 10 ' AB\ 00 01 ' 11 10
1 I I I I I I
1
00 [[1 1 1J ^ 00
0 1 ^ 3 2
01 <f) 1 1 ^1 01
4 5 7 6
11 1 1 V 11
- 12 13 15 W 13
A A
10 f 1 ~$\ 10
|^— ' 8 9 11 10/
/ Y
D D
ORIGINAL largest grouping of Pis REDUCE - 4 Pis
(Similar to Q-M PI table).
(a) (b)

\CD C \CD C
AB\ 00 01 11 10 AB\ 00 01 11 10
00 (7| 1 <t> 00 1 ~H (f)
0 1 3 2 n 0 1 3 2
— J 1 1 1) /• — \
01 01 1
Y 4 5 1 6 ^ 4 5 7
._ B p - 5
11 1 (1 O 11 1 J_ __J
A 12 13 15 14 A 12 13 15 14
10 1 10 1
\ f s ^ 9 11 10/ 8 ^ 9 11 10 /
/ Y / *
D D
EXPAND - 4 Pis IRREDUNDANT COVER
(Eliminates ABC, ACD) (Eliminates ABC)
(c) (d)
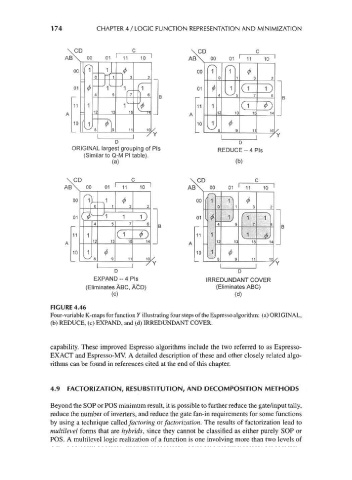
FIGURE 4.46
Four-variable K-maps for function Y illustrating four steps of the Espresso algorithm: (a) ORIGINAL,
(b) REDUCE, (c) EXPAND, and (d) IRREDUNDANT COVER.

capability. These improved Espresso algorithms include the two referred to as Espresso-
EXACT and Espresso-MV. A detailed description of these and other closely related algo-
rithms can be found in references cited at the end of this chapter.

4.9 FACTORIZATION, RESUBSTITUTION, AND DECOMPOSITION METHODS

Beyond the SOP or POS minimum result, it is possible to further reduce the gate/input tally,
reduce the number of inverters, and reduce the gate fan-in requirements for some functions
by using a technique called factoring or factorization. The results of factorization lead to
multilevel forms that are hybrids, since they cannot be classified as either purely SOP or
POS. A multilevel logic realization of a function is one involving more than two levels of