Page 115 - Engineering Electromagnetics, 8th Edition

CHAPTER 4 Energy and Potential 97

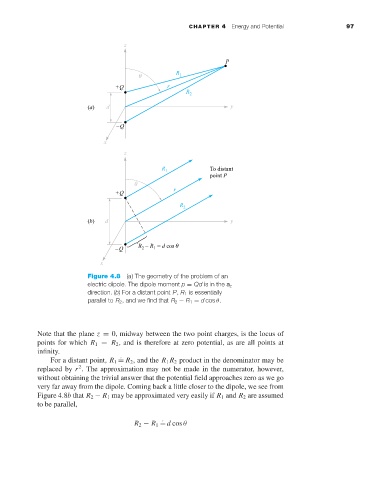
Figure 4.8 (a) The geometry of the problem of an
electric dipole. The dipole moment p = Qd is in the a z
direction. (b) For a distant point P, R 1 is essentially
parallel to R 2 , and we find that R 2 − R 1 = d cos θ.

Note that the plane z = 0, midway between the two point charges, is the locus of
points for which R 1 = R 2 , and is therefore at zero potential, as are all points at
infinity.
Fora distant point, R 1 ˙= R 2 , and the R 1 R 2 product in the denominator may be
2
replaced by r . The approximation may not be made in the numerator, however,
without obtaining the trivial answer that the potential field approaches zero as we go
very far away from the dipole. Coming back a little closer to the dipole, we see from
Figure 4.8b that R 2 − R 1 may be approximated very easily if R 1 and R 2 are assumed
to be parallel,

R 2 − R 1 ˙= d cos θ