Page 140 - Engineering Electromagnetics, 8th Edition

122 ENGINEERING ELECTROMAGNETICS

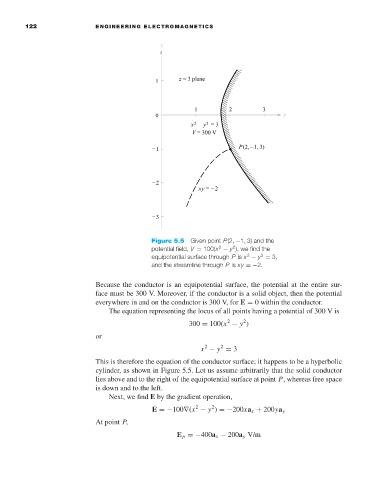
Figure 5.5 Given point P(2, −1, 3) and the
2
potential field, V = 100(x − y ), we find the
2
2
2
equipotential surface through P is x − y = 3,
and the streamline through P is xy =−2.
Because the conductor is an equipotential surface, the potential at the entire sur-
face must be 300 V. Moreover, if the conductor is a solid object, then the potential
everywhere in and on the conductor is 300 V, for E = 0 within the conductor.
The equation representing the locus of all points having a potential of 300 V is
2
2
300 = 100(x − y )
or
2
2
x − y = 3
This is therefore the equation of the conductor surface; it happens to be a hyperbolic
cylinder, as shown in Figure 5.5. Let us assume arbitrarily that the solid conductor
lies above and to the right of the equipotential surface at point P, whereas free space
is down and to the left.
Next, we find E by the gradient operation,
2 2
E =−100∇(x − y ) =−200xa x + 200ya y
At point P,

E p =−400a x − 200a y V/m