Page 523 - Engineering Electromagnetics, 8th Edition

CHAPTER 13 Guided Waves 505

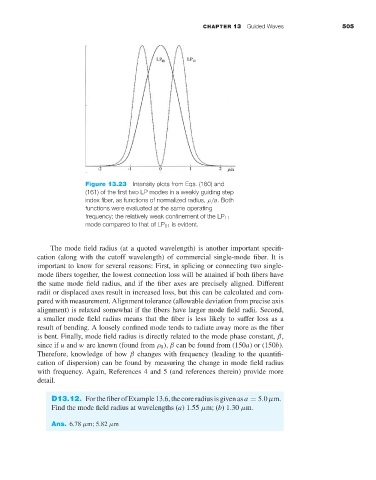
Figure 13.23 Intensity plots from Eqs. (160) and
(161) of the first two LP modes in a weakly guiding step
index fiber, as functions of normalized radius, ρ/a. Both
functions were evaluated at the same operating
frequency; the relatively weak confinement of the LP 11
mode compared to that of LP 01 is evident.

The mode field radius (at a quoted wavelength) is another important specifi-
cation (along with the cutoff wavelength) of commercial single-mode fiber. It is
important to know for several reasons: First, in splicing or connecting two single-
mode fibers together, the lowest connection loss will be attained if both fibers have
the same mode field radius, and if the fiber axes are precisely aligned. Different
radii or displaced axes result in increased loss, but this can be calculated and com-
pared with measurement. Alignment tolerance (allowable deviation from precise axis
alignment) is relaxed somewhat if the fibers have larger mode field radii. Second,
a smaller mode field radius means that the fiber is less likely to suffer loss as a
result of bending. A loosely confined mode tends to radiate away more as the fiber
is bent. Finally, mode field radius is directly related to the mode phase constant, β,
since if u and w are known (found from ρ 0 ),β can be found from (150a)or (150b).
Therefore, knowledge of how β changes with frequency (leading to the quantifi-
cation of dispersion) can be found by measuring the change in mode field radius
with frequency. Again, References 4 and 5 (and references therein) provide more
detail.

D13.12. ForthefiberofExample13.6,thecoreradiusisgivenasa = 5.0µm.
Find the mode field radius at wavelengths (a) 1.55 µm; (b) 1.30 µm.

Ans. 6.78 µm; 5.82 µm