Page 538 - Engineering Electromagnetics, 8th Edition

520 ENGINEERING ELECTROMAGNETICS

2
dA = r dW = r sinqdq df
2
q

dW
r

f

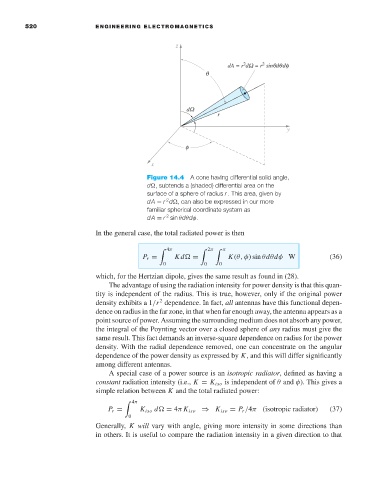
Figure 14.4 A cone having differential solid angle,
d
, subtends a (shaded) differential area on the
surface of a sphere of radius r . This area, given by
2
dA = r d
, can also be expressed in our more
familiar spherical coordinate system as
2
dA = r sin θdθdφ.
In the general case, the total radiated power is then

4π 2π π
K(θ, φ) sin θdθdφ W (36)
P r = Kd
=
0 0 0
which, for the Hertzian dipole, gives the same result as found in (28).
The advantage of using the radiation intensity for power density is that this quan-
tity is independent of the radius. This is true, however, only if the original power
2
density exhibits a 1/r dependence. In fact, all antennas have this functional depen-
dence on radius in the far zone, in that when far enough away, the antenna appears as a
point source of power. Assuming the surrounding medium does not absorb any power,
the integral of the Poynting vector over a closed sphere of any radius must give the
same result. This fact demands an inverse-square dependence on radius for the power
density. With the radial dependence removed, one can concentrate on the angular
dependence of the power density as expressed by K, and this will differ significantly
among different antennas.
A special case of a power source is an isotropic radiator, defined as having a
constant radiation intensity (i.e., K = K iso is independent of θ and φ). This gives a
simple relation between K and the total radiated power:

4π

K iso d
= 4π K iso ⇒ K iso = P r /4π (isotropic radiator) (37)
P r =
0
Generally, K will vary with angle, giving more intensity in some directions than
in others. It is useful to compare the radiation intensity in a given direction to that