Page 102 - Entrophy Analysis in Thermal Engineering Systems

Irreversible engines—Closed cycles 95

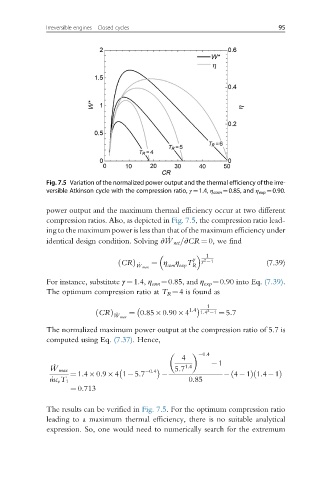
Fig. 7.5 Variation of the normalized power output and the thermal efficiency of the irre-
versible Atkinson cycle with the compression ratio, γ ¼1.4, η com ¼0.85, and η exp ¼0.90.

power output and the maximum thermal efficiency occur at two different
compression ratios. Also, as depicted in Fig. 7.5, the compression ratio lead-
ing to the maximum power is less than that of the maximum efficiency under
identical design condition. Solving ∂ _ W net =∂CR ¼ 0, we find

1

γ γ 1
2
ð ¼ η η T (7.39)
com exp R
CRÞ _ W max
For instance, substitute γ ¼1.4, η com ¼0.85, and η exp ¼0.90 into Eq. (7.39).
The optimum compression ratio at T R ¼4 is found as
1
1:4
2
ð CRÞ _ W max ¼ 0:85 0:90 4 1:4 1 ¼ 5:7
The normalized maximum power output at the compression ratio of 5.7 is
computed using Eq. (7.37). Hence,

0:4
4
1
5:7 1:4
0:4
¼ 1:4 0:9 41 5:7 4 1Þ 1:4 1Þ
_ W max
ð
ð
_ mc v T 1 0:85
¼ 0:713
The results can be verified in Fig. 7.5. For the optimum compression ratio
leading to a maximum thermal efficiency, there is no suitable analytical
expression. So, one would need to numerically search for the extremum