Page 103 - Entrophy Analysis in Thermal Engineering Systems

96 Entropy Analysis in Thermal Engineering Systems

of the efficiency given in Eq. (7.38). For example, with the above values of
γ, η com , η exp , and T R , the maximum thermal efficiency is found to be
0.328 using the Golden-Section Search method, which occurs at a compres-
sion ratio of 8.6.
The total entropy generation rate is determined by substituting
Eqs. (7.35) and (7.36) into Eq. (7.14). Hence,

γ 1 γ
_
Φ ð T R CR Þ 1 1 γ
¼ + γη T R CR 1
_ mc v T 1 =T L Þ η π exp
ð
com
(7.40)
1
+ T R 1ð Þ γ
π
The optimum compression ratio leading to a minimum entropy generation
_
rate is obtained by solving ∂Φ =∂CR ¼ 0.
1 1

γ
¼ η η T π γ 1 γ 1
2
2
ð ð π ðÞ (7.41)
com exp R ¼ CRÞ _ W max
CRÞ _ Φ min
For γ ¼1.4, we have 1 1. So, it can be deduced from Eq. (7.41) that the
2
γ 1
compression ratio at minimum entropy generation rate is about π times
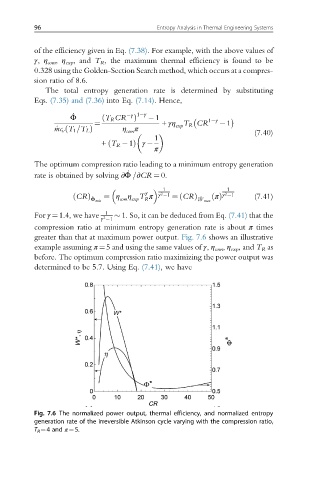
greater than that at maximum power output. Fig. 7.6 shows an illustrative
example assuming π ¼5 and using the same values of γ, η com , η exp , and T R as
before. The optimum compression ratio maximizing the power output was
determined to be 5.7. Using Eq. (7.41), we have

Fig. 7.6 The normalized power output, thermal efficiency, and normalized entropy
generation rate of the irreversible Atkinson cycle varying with the compression ratio,
T R ¼4 and π ¼5.