Page 79 - Entrophy Analysis in Thermal Engineering Systems

Endoreversible heat engines 71

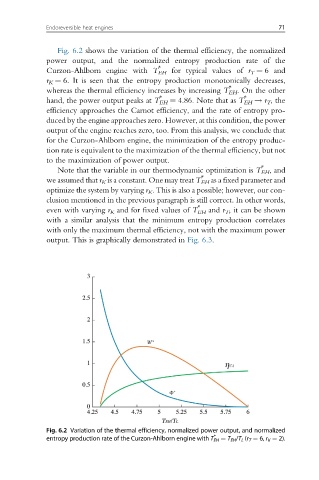
Fig. 6.2 shows the variation of the thermal efficiency, the normalized
power output, and the normalized entropy production rate of the
∗
Curzon-Ahlborn engine with T EH for typical values of r T ¼ 6 and
r K ¼ 6. It is seen that the entropy production monotonically decreases,
∗
whereas the thermal efficiency increases by increasing T EH . On the other
∗ ∗
hand, the power output peaks at T EH ¼ 4.86. Note that as T EH ! r T , the
efficiency approaches the Carnot efficiency, and the rate of entropy pro-
duced by the engine approaches zero. However, at this condition, the power
output of the engine reaches zero, too. From this analysis, we conclude that
for the Curzon-Ahlborn engine, the minimization of the entropy produc-
tion rate is equivalent to the maximization of the thermal efficiency, but not
to the maximization of power output.
∗
Note that the variable in our thermodynamic optimization is T EH , and
∗
we assumed that r K is a constant. One may treat T EH as a fixed parameter and
optimize the system by varying r K . This is also a possible; however, our con-
clusion mentioned in the previous paragraph is still correct. In other words,
∗
even with varying r K and for fixed values of T EH and r T , it can be shown
with a similar analysis that the minimum entropy production correlates
with only the maximum thermal efficiency, not with the maximum power
output. This is graphically demonstrated in Fig. 6.3.

Fig. 6.2 Variation of the thermal efficiency, normalized power output, and normalized
∗
entropy production rate of the Curzon-Ahlborn engine with T EH ¼ T EH /T L (r T ¼ 6, r K ¼ 2).