Page 81 - Entrophy Analysis in Thermal Engineering Systems

Endoreversible heat engines 73

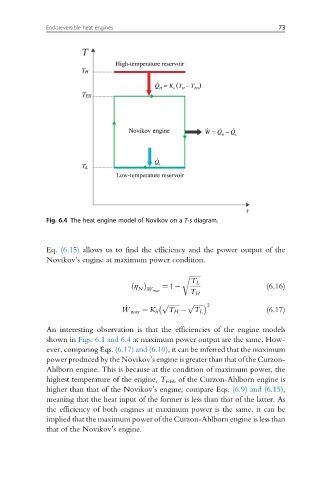
Fig. 6.4 The heat engine model of Novikov on a T-s diagram.

Eq. (6.15) allows us to find the efficiency and the power output of the
Novikov’s engine at maximum power condition.

r ffiffiffiffiffiffiffi
T L
η ð N W max ¼ 1 T H (6.16)
Þ _
p p ffiffiffiffiffiffi 2
_ ffiffiffiffiffiffiffi (6.17)

T H T L
W max ¼ K h
An interesting observation is that the efficiencies of the engine models
shown in Figs. 6.1 and 6.4 at maximum power output are the same. How-
ever, comparing Eqs. (6.17) and (6.10), it can be inferred that the maximum
power produced by the Novikov’s engine is greater than that of the Curzon-
Ahlborn engine. This is because at the condition of maximum power, the
highest temperature of the engine, T EH , of the Curzon-Ahlborn engine is
higher than that of the Novikov’s engine; compare Eqs. (6.9) and (6.15),
meaning that the heat input of the former is less than that of the latter. As
the efficiency of both engines at maximum power is the same, it can be
implied that the maximum power of the Curzon-Ahlborn engine is less than
that of the Novikov’s engine.