Page 80 - Entrophy Analysis in Thermal Engineering Systems

72 Entropy Analysis in Thermal Engineering Systems

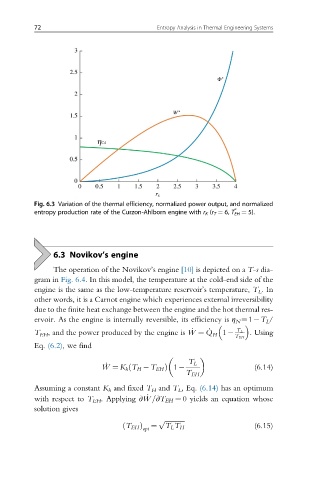
Fig. 6.3 Variation of the thermal efficiency, normalized power output, and normalized
∗
entropy production rate of the Curzon-Ahlborn engine with r K (r T ¼ 6, T EH ¼ 5).

6.3 Novikov’s engine

The operation of the Novikov’s engine [10] is depicted on a T-s dia-
gram in Fig. 6.4. In this model, the temperature at the cold-end side of the
engine is the same as the low-temperature reservoir’s temperature, T L .In
other words, it is a Carnot engine which experiences external irreversibility
due to the finite heat exchange between the engine and the hot thermal res-
ervoir. As the engine is internally reversible, its efficiency is η N ¼1 T L /

_
T EH , and the power produced by the engine is _ W ¼ Q 1 T L . Using
H T EH
Eq. (6.2), we find

T L
ð
_ W ¼ K h T H T EH Þ 1 T EH (6.14)
Assuming a constant K h and fixed T H and T L , Eq. (6.14) has an optimum
_
with respect to T EH . Applying ∂W =∂T EH ¼ 0 yields an equation whose
solution gives
p ffiffiffiffiffiffiffiffiffiffiffiffi
ð (6.15)
T EH Þ ¼ T L T H
opt