Page 159 - Essentials of physical chemistry

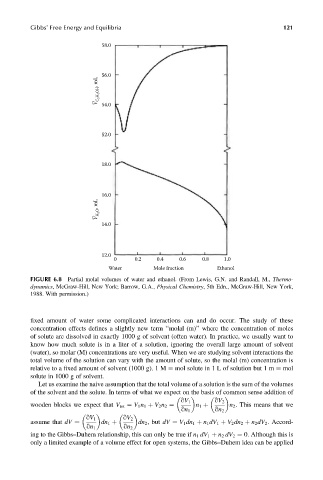
Gibbs’ Free Energy and Equilibria 121

58.0

56.0
V C 2 H 2 OH , mL

–
54.0

52.0

18.0

16.0
V H 2O , mL

–
14.0

12.0
0 0.2 0.4 0.6 0.8 1.0
Water Mole fraction Ethanol
FIGURE 6.8 Partial molal volumes of water and ethanol. (From Lewis, G.N. and Randall, M., Thermo-
dynamics, McGraw-Hill, New York; Barrow, G.A., Physical Chemistry, 5th Edn., McGraw-Hill, New York,
1988. With permission.)

fixed amount of water some complicated interactions can and do occur. The study of these
concentration effects defines a slightly new term ‘‘molal (m)’’ where the concentration of moles
of solute are dissolved in exactly 1000 g of solvent (often water). In practice, we usually want to
know how much solute is in a liter of a solution, ignoring the overall large amount of solvent
(water), so molar (M) concentrations are very useful. When we are studying solvent interactions the
total volume of the solution can vary with the amount of solute, so the molal (m) concentration is
relative to a fixed amount of solvent (1000 g). 1 M mol solute in 1 L of solution but 1 m mol
solute in 1000 g of solvent.
Let us examine the naive assumption that the total volume of a solution is the sum of the volumes
of the solvent and the solute. In terms of what we expect on the basis of common sense addition of

qV 1 qV 2
n 2 . This means that we
wooden blocks we expect that V tot ¼ V 1 n 1 þ V 2 n 2 ¼ n 1 þ
qn 1 qn 2

qV 1 qV 2
dn 2 , but dV ¼ V 1 dn 1 þ n 1 dV 1 þ V 2 dn 2 þ n 2 dV 2 . Accord-
assume that dV ¼ dn 1 þ
qn 1 qn 2
ing to the Gibbs–Duhem relationship, this can only be true if n 1 dV 1 þ n 2 dV 2 ¼ 0. Although this is
only a limited example of a volume effect for open systems, the Gibbs–Duhem idea can be applied