Page 60 - Essentials of physical chemistry

22 Essentials of Physical Chemistry

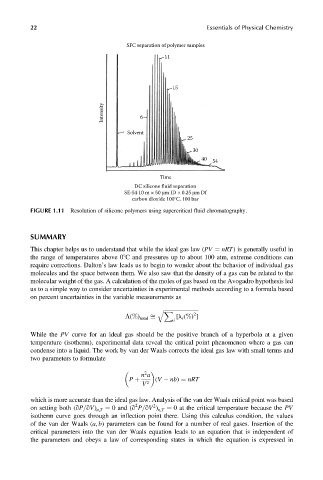
SFC separation of polymer samples
11

15

Intensity 6

Solvent
25
30
40
54
Time
DC silicone fluid separation
SE-54 10 m × 50 μm ID × 0.25 μm Df
carbon dioxide 100°C, 100 bar
FIGURE 1.11 Resolution of silicone polymers using supercritical fluid chromatography.

SUMMARY
This chapter helps us to understand that while the ideal gas law (PV ¼ nRT) is generally useful in
the range of temperatures above 08C and pressures up to about 100 atm, extreme conditions can
require corrections. Dalton’s law leads us to begin to wonder about the behavior of individual gas
molecules and the space between them. We also saw that the density of a gas can be related to the
molecular weight of the gas. A calculation of the moles of gas based on the Avogadro hypothesis led
us to a simple way to consider uncertainties in experimental methods according to a formula based
on percent uncertainties in the variable measurements as

q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
X 2
[l i (%) ]
i
L(%) total ffi
While the PV curve for an ideal gas should be the positive branch of a hyperbola at a given
temperature (isotherm), experimental data reveal the critical point phenomenon where a gas can
condense into a liquid. The work by van der Waals corrects the ideal gas law with small terms and
two parameters to formulate

2
n a
(V nb) ¼ nRT
P þ 2
V
which is more accurate than the ideal gas law. Analysis of the van der Waals critical point was based
2
2
on setting both (qP=qV) n,T ¼ 0 and (q P=qV ) n,T ¼ 0 at the critical temperature because the PV
isotherm curve goes through an inflection point there. Using this calculus condition, the values
of the van der Waals (a, b) parameters can be found for a number of real gases. Insertion of the
critical parameters into the van der Waals equation leads to an equation that is independent of
the parameters and obeys a law of corresponding states in which the equation is expressed in