Page 55 - Essentials of physical chemistry

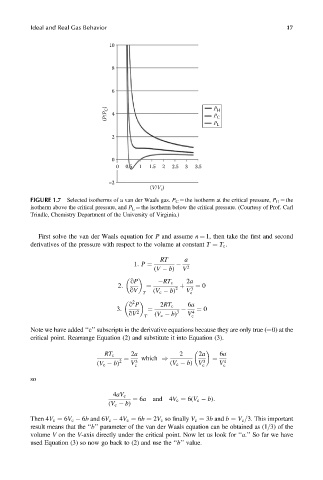
Ideal and Real Gas Behavior 17

10

8

6

(P/P C ) 4 P H C
P
P L
2

0
0 0.5 1 1.5 2 2.5 3 3.5

–2
(V/V )
c
FIGURE 1.7 Selected isotherms of a van der Waals gas. P C ¼ the isotherm at the critical pressure, P H ¼ the
isotherm above the critical pressure, and P L ¼ the isotherm below the critical pressure. (Courtesy of Prof. Carl
Trindle, Chemistry Department of the University of Virginia.)

First solve the van der Waals equation for P and assume n ¼ 1, then take the first and second
derivatives of the pressure with respect to the volume at constant T ¼ T c .
RT a
1: P ¼ 2
(V b) V

qP RT c 2a
2: ¼ þ ¼ 0
qV (V c b) 2 V 3
T c
2
q P 2RT c 6a
3: ¼ ¼ 0
qV 2 (V c b) 3 V 4
T c
Note we have added ‘‘c’’ subscripts in the derivative equations because they are only true (¼0) at the
critical point. Rearrange Equation (2) and substitute it into Equation (3).

2a 2 2a 6a
RT c
(V c b) 2 ¼ V c 3 which ) (V c b) V c 3 ¼ V c 4
so

4aV c
¼ 6a and 4V c ¼ 6(V c b):
(V c b)
Then 4V c ¼ 6V c 6b and 6V c 4V c ¼ 6b ¼ 2V c so finally V c ¼ 3b and b ¼ V c =3. This important
result means that the ‘‘b’’ parameter of the van der Waals equation can be obtained as (1=3) of the
volume V on the V-axis directly under the critical point. Now let us look for ‘‘a.’’ So far we have
used Equation (3) so now go back to (2) and use the ‘‘b’’ value.