Page 83 - Essentials of physical chemistry

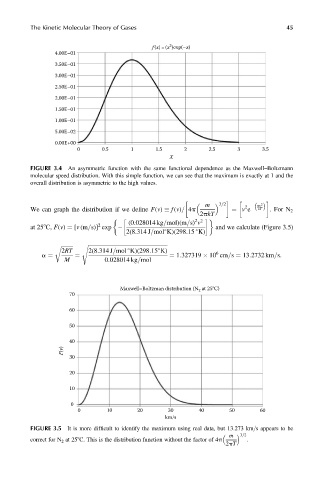
The Kinetic Molecular Theory of Gases 45

2
f (x)=(x )exp(–x)
4.00E–01
3.50E–01
3.00E–01
2.50E–01
2.00E–01
1.50E–01
1.00E–01
5.00E–02
0.00E+00
0 0.5 1 1.5 2 2.5 3 3.5
X
FIGURE 3.4 An asymmetric function with the same functional dependence as the Maxwell–Boltzmann
molecular speed distribution. With this simple function, we can see that the maximum is exactly at 1 and the
overall distribution is asymmetric to the high values.

m
3=2 mv 2
We can graph the distribution if we define F(v) f (v)= 4p ¼ v e kT .For N 2
2
2pkT
2 2
(0:028014 kg=mol)(m=s) v
2
at 258C, F(v) ¼ [v (m=s)] exp and we calculate (Figure 3.5)
2(8:314 J=mol K)(298:15 K)

s ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ffiffiffiffiffiffiffiffiffi
2RT 2(8:314 J=mol K)(298:15 K) 6

¼ 1:327319 10 cm=s ¼ 13:2732 km=s:
a ¼ ¼
M 0:028014 kg=mol
Maxwell–Boltzman distribution (N at 25°C)
2
70
60
50
40
F(v)
30

20

10

0
0 10 20 30 40 50 60
km/s
FIGURE 3.5 It is more difficult to identify the maximum using real data, but 13.273 km=s appears to be
m
3=2
correct for N 2 at 258C. This is the distribution function without the factor of 4p .
2pT