Page 156 - Excel for Scientists and Engineers: Numerical Methods

CHAPTER 7 INTEGRATION 133

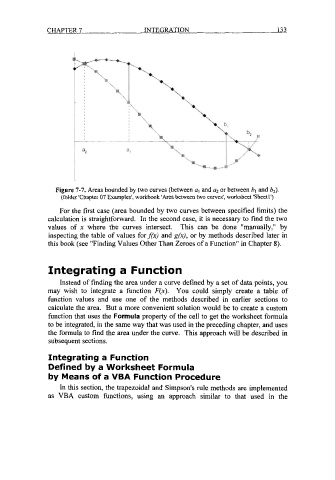
Figure 7-7. Areas bounded by two curves (between al and q or between b, and b2).
(folder 'Chapter 07 Examples', workbook 'Area between two curves', worksheet 'Sheetl')

For the first case (area bounded by two curves between specified limits) the
calculation is straightforward. In the second case, it is necessary to find the two
values of x where the curves intersect. This can be done "manually," by
inspecting the table of values forf(x) and g($, or by methods described later in
this book (see "Finding Values Other Than Zeroes of a Function'' in Chapter 8).

Integrating a Function
Instead of finding the area under a curve defined by a set of data points, you
may wish to integrate a function F(x). You could simply create a table of
function values and use one of the methods described in earlier sections to
calculate the area. But a more convenient solution would be to create a custom
function that uses the Formula property of the cell to get the worksheet formula
to be integrated, in the same way that was used in the preceding chapter, and uses
the formula to find the area under the curve. This approach will be described in
subsequent sections.

Integrating a Function
Defined by a Worksheet Formula
by Means of a VBA Function Procedure
In this section, the trapezoidal and Simpson's rule methods are implemented
as VBA custom functions, using an approach similar to that used in the