Page 270 - Excel for Scientists and Engineers: Numerical Methods

CHAPTER 11 ORDINARY DIFFERENTIAL EOUATIONS. PART I1 247

We want to calculate the amount of deflection of the beam at the center of
the span. Since the deflection is known to be zero at either end of the beam 0, =
0 at x = 0 and y = 0 at x = 30), this is a boundary value problem. We will solve it
by using the shooting method. We set up the problem as though it were an
initial-value problem, with two "knowns" given at the same boundary, x = 0 in
this example. The two known values are the value of y at x = 0 and a trial value
ofz at x = 0.
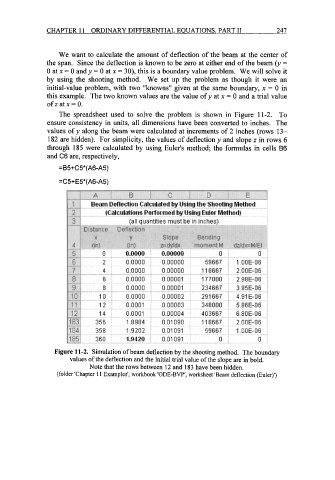
The spreadsheet used to solve the problem is shown in Figure 11-2. To
ensure consistency in units, all dimensions have been converted to inches. The
values of y along the beam were calculated at increments of 2 inches (rows 13-
182 are hidden). For simplicity, the values of deflection y and slope z in rows 6
through 185 were calculated by using Euler's method; the formulas in cells B6
and C6 are, respectively,
=B5+C5*(A6-A5)
=C5+E5*(A6-A5)

Figure 11-2. Simulation of beam deflection by the shooting method. The boundary
values of the deflection and the initial trial value of the slope are in bold.
Note that the rows between 12 and 183 have been hidden.
(folder 'Chapter 1 1 Examples', workbook 'ODE-BVP, worksheet 'Beam deflection (Euler)')