Page 374 - Excel for Scientists and Engineers: Numerical Methods

CHAPTER 15 RANDOM NUMBERS & MONTE CARL0 METHOD 351

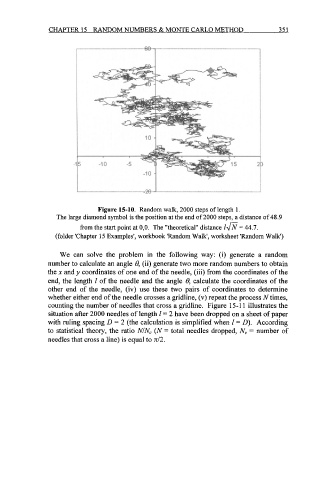
Figure 15-10. Random walk, 2000 steps of length 1.
The large diamond symbol is the position at the end of 2000 steps, a distance of 48.9
from the start point at 0,O. The "theoretical" distance 1fi = 44.7.
(folder 'Chapter 15 Examples', workbook 'Random Walk', worksheet 'Random Walk')

We can solve the problem in the following way: (i) generate a random
number to calculate an angle 8, (ii) generate two more random numbers to obtain
the x and y coordinates of one end of the needle, (iii) from the coordinates of the
end, the length 1 of the needle and the angle 8, calculate the coordinates of the
other end of the needle, (iv) use these two pairs of coordinates to determine
whether either end of the needle crosses a gridline, (v) repeat the process N times,
counting the number of needles that cross a gridline. Figure 15-1 1 illustrates the
situation after 2000 needles of length 1 = 2 have been dropped on a sheet of paper
with ruling spacing D = 2 (the calculation is simplified when 1 = 0). According
to statistical theory, the ratio N/Nc (N = total needles dropped, N, = number of
needles that cross a line) is equal to 7d2.