Page 512 - Fair, Geyer, and Okun's Water and wastewater engineering : water supply and wastewater removal

JWCL344_ch13_457-499.qxd 8/7/10 8:49 PM Page 470

470 Chapter 13 Hydraulics of Sewer Systems

C of manhole
1
Energy grade line

h velocity head h e
v 1
Water surface hydraulic 2
grade line slope s 1 h
v velocity h 1 d depth of flow 8
1
1
a cross-sectional area
1
q a v rate of flow
1
1 1
h
h v 2
Sewer gradient, slope i 1 i
s 2
d 2
h 2 v 2
i 2
a 2
q 2
Uniform flow Transition Uniform flow

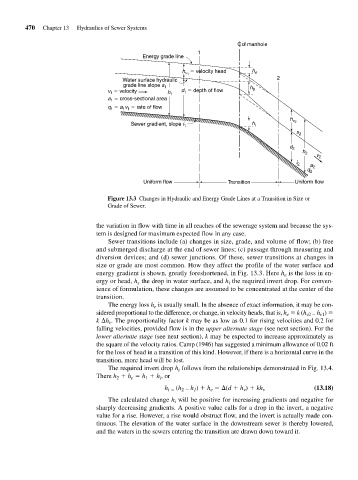
Figure 13.3 Changes in Hydraulic and Energy Grade Lines at a Transition in Size or
Grade of Sewer.

the variation in flow with time in all reaches of the sewerage system and because the sys-
tem is designed for maximum expected flow in any case.
Sewer transitions include (a) changes in size, grade, and volume of flow; (b) free
and submerged discharge at the end of sewer lines; (c) passage through measuring and
diversion devices; and (d) sewer junctions. Of these, sewer transitions at changes in
size or grade are most common. How they affect the profile of the water surface and
energy gradient is shown, greatly foreshortened, in Fig. 13.3. Here h is the loss in en-
e
ergy or head, h the drop in water surface, and h the required invert drop. For conven-
s
i
ience of formulation, these changes are assumed to be concentrated at the center of the
transition.
The energy loss h is usually small. In the absence of exact information, it may be con-
e
sidered proportional to the difference, or change, in velocity heads, that is, h k (h v2 v1
h )
e
k h . The proportionality factor k may be as low as 0.1 for rising velocities and 0.2 for
v
falling velocities, provided flow is in the upper alternate stage (see next section). For the
lower alternate stage (see next section), k may be expected to increase approximately as
the square of the velocity ratios. Camp (1946) has suggested a minimum allowance of 0.02 ft
for the loss of head in a transition of this kind. However, if there is a horizontal curve in the
transition, more head will be lost.
The required invert drop h follows from the relationships demonstrated in Fig. 13.4.
i
There h h h h , or
1
e
2
i
h ) h (d h ) kh
h i (h 2 1 e v v (13.18)
The calculated change h will be positive for increasing gradients and negative for
i
sharply decreasing gradients. A positive value calls for a drop in the invert, a negative
value for a rise. However, a rise would obstruct flow, and the invert is actually made con-
tinuous. The elevation of the water surface in the downstream sewer is thereby lowered,
and the waters in the sewers entering the transition are drawn down toward it.