Page 88 - Fair, Geyer, and Okun's Water and wastewater engineering : water supply and wastewater removal

JWCL344_ch02_029-060.qxd 8/2/10 9:14 PM Page 51

2.11 Spillways 51

b

Plan

z
1
2
b b h v /2g
v
h
h v
H d

Longitudinal section
(a) (b)
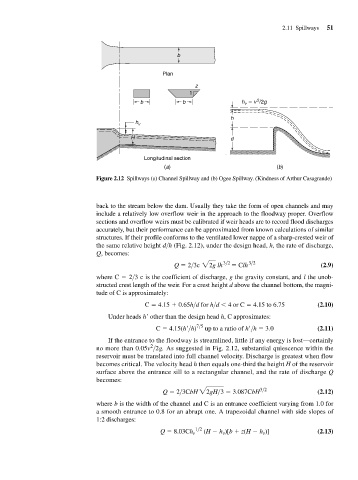
Figure 2.12 Spillways (a) Channel Spillway and (b) Ogee Spillway. (Kindness of Arthur Casagrande)

back to the stream below the dam. Usually they take the form of open channels and may
include a relatively low overflow weir in the approach to the floodway proper. Overflow
sections and overflow weirs must be calibrated if weir heads are to record flood discharges
accurately, but their performance can be approximated from known calculations of similar
structures. If their profile conforms to the ventilated lower nappe of a sharp-crested weir of
the same relative height d>h (Fig. 2.12), under the design head, h, the rate of discharge,
Q, becomes:
Q 2>3c 22g lh 3>2 Clh 3>2 (2.9)

where C 2>3 c is the coefficient of discharge, g the gravity constant, and l the unob-
structed crest length of the weir. For a crest height d above the channel bottom, the magni-
tude of C is approximately:
C 4.15 0.65h>d for h>d 4 or C 4.15 to 6.75 (2.10)
Under heads h
other than the design head h, C approximates:
C 4.15(h
>h) 7>5 up to a ratio of h
>h 3.0 (2.11)

If the entrance to the floodway is streamlined, little if any energy is lost—certainly
2
no more than 0.05v >2g. As suggested in Fig. 2.12, substantial quiescence within the
reservoir must be translated into full channel velocity. Discharge is greatest when flow
becomes critical. The velocity head h then equals one-third the height H of the reservoir
surface above the entrance sill to a rectangular channel, and the rate of discharge Q
becomes:
Q 2>3CbH 22gH>3 3.087CbH 3>2 (2.12)

where b is the width of the channel and C is an entrance coefficient varying from 1.0 for
a smooth entrance to 0.8 for an abrupt one. A trapezoidal channel with side slopes of
1:2 discharges:
Q 8.03Ch v 1>2 (H h )[b z(H h )] (2.13)
v
v